Լոգարիթմ
Լոգարիթմ (հունարեն՝ λόγος - «հարաբերություն» և ἀριθμός - «թիվ»)[1], թվի լոգարիթմ հիմքով, որտեղ , այն թիվը, որով պետք է աստիճան բարձրացնել հիմքը թիվը ստանալու համար[2]։
Այն նշանակում են տեսքով և կարդում «լոգարիթմ հիմքով »։
Սահմանումից հետևում է, որ հավասարումը համարժեք է հավասարմանը։
Լոգարիթմի հաշվումը հաճախ անվանում են լոգարիթմում։
և թվերը հաճախ իրական թվեր են, սակայն կան նաև կոմպլեքս լոգարիթմներ։
Լոգարիթմները օժտված են յուրահատուկ հատկություններով, որոնք սահմանել են նրա լայն կիրառությունը դժվարին հաշվարկների հնարավոր պարզեցման մեջ[3]։ «Լոգարիթմների աշխարհում» բազմապատկումը փոխարինվում է շատ ավելի պարզ գումարմամբ, բաժանումը՝ հանմամբ, իսկ աստիճան բարձրացնելը և արմատ հանելը համապատասխանաբար փոխակերպվում են բազմապատկման և բաժանման աստիճանի ցուցիչի վրա։ Պիեր Սիմոն Լապլասը ասել է, որ լոգարիթմների հայտնագործումը՝ «կրճատելով աստղագետի աշխատանքը, կրկնապատկել է նրա կյանքը»[4]։
Լոգարիթմների սահմանումը և նրանց նշանակությունների աղյուսակը (եռանկյունաչափական ֆունկցիաների համար) առաջին անգամ հրապարակել է շոտլանդացի մաթեմատիկոս Ջոն Նեպերը 1614 թվականին։ Լոգարիթմական աղյուսակները, ընդարձակված և ճշգրտված այլ մաթեմատիկոսների կողմից, համատարած օգտագործվում էին գիտական և ճարտարագիտական հաշվարկների համար ավելի քան երեք դար, մինչև հայտնվեցին էլեկտրոնային հաշվիչներն ու համակարգիչները։
Ժամանակի ընթացքում պարզվել է, որ լոգարիթմական ֆունկցիան անփոխարինելի է նաև մարդկային գործունեության այլ բնագավառների համար, այդ թվում՝ դիֆֆերենցիալ հավասարումների լուծման, մեծությունների նշանակությունների դասակարգման (օրինակ՝ հաճախականություն և ձայնի ինտենսիվություն), տարբեր կախույթների ապրոկսիմացիայի, տեղեկության տեսությունների, հավանականության տեսությունների և այլն։ Այս ֆունկցիան պատկանում է տարրականների շարքին, այն հակադարձ համեմատական է տիպային ֆունկցիային։ Ամենից հաճախ օգտագործվում են իրական լոգարիթմները հիմքով (բնական լոգարիթմ), հիմքով և հիմքով։
Իրական լոգարիթմներ
խմբագրելԻրական թվի լոգարիթմը, ըստ սահմանման, հավասարման լուծումն է։ դեպքը հետաքրքրություն չի ներկայացնում, քանի որ այդ ժամանակ այս հավասարումը լուծում չունի, իսկ դեպքում ցանկացած թիվ լուծում է. երկու դեպքում էլ լոգարիթմը որոշված չէ։ Նմանապես եզրակացնում ենք, որ լոգարիթմը գոյություն չունի զրոյական կամ բացասական -ի դեպքում։ Բացի այդ, ցուցչային ֆունկցիայի արժեքը միշտ դրական է, ուստի պետք է բացառել նաև բացասական -ի դեպքը։ Արդյունքում ստանում ենք[5].
արտահայտությունը որոշված է այն և միայն այն դեպքում, երբ
Ինչպես հայտնի է, ֆունկցիան ( -ի համար նշված պայմանների կատարման դեպքում) գոյություն ունի, մոնոտոն է և յուրաքանչյուր արժեք ընդունում է միայն մեկ անգամ, ընդ որում՝ դրա արժեքների տիրույթը պարունակում է բոլոր դրական իրական թվերը[6]։ Սրանից հետևում է, որ դրական թվի իրական լոգարիթմի արժեքը միշտ գոյություն ունի և միանշանակ որոշված է։
Լայն կիրառություն ունեն հետևյալ տեսքի լոգարիթմները.
- Բնական. հիմքը հանդիսանում է Էյլերի թիվը (e),
- Տասնորդական. , հիմքը հանդիսանում է -ը,
- Երկուական. , հիմքը հանդիսանում է -ը։
Սրանք լայն կիրառություն ունեն, օրինակ, ինֆորմատիկայում, դիսկրետ մաթեմատիկայի շատ բաժիններում և այլն։
Հատկություններ
խմբագրելՀիմնական լոգարիթմական նույնություններ
խմբագրելԼոգարիթմի սահմանումից հետևում է հիմնական լոգարիթմական նույնութըունը. Ապացուցում։ Եթե , ապա , որտեղից հետևում է, որ ։
Լոգարիթմի միավորը և թիվը
| Բանաձև | Օրինակ | |
|---|---|---|
| Արտադրյալ | ||
| Քանորդ | ||
| Աստիճան | ||
| Արմատ |
Կա ակնհայտ ընդհանրացում բանաձևերի, որը տրվում է այն դեպքում, երբ թույլատրվում է բացասական արժեքների փոփոխումներ, օրինակ
Արտադրյալի լոգարիթմի բանաձևերը հեշտությամբ ընդհանրացվում են կամայական թվով արտադրիչների համար։
Վերոնշյալ հատկությունները բացատրում են, թե ինչու լոգարիթմների կիրառությունը (մինչև հաշվիչների հայտնագործումը) անչափ հեշտացնում է հաշվարկները։ Օրինակ, բազմանիշ թվերի արտադրյալը լոգարիթմական աղյուսակի օգնությամբ կատարվում է հետևյալ ալգորիթմով՝
- լոգարիթմների աղյուսակում գտնում ենք թվերը,
- գումարում ենք այդ լոգարիթմները, ստանում ենք (համաձայն առաջին հատկության) արտադրյալի լոգարիթմը,
- ըստ արտադրյալի լոգարիթմի աղյուսակներում գտնում ենք հենց արտադրյալը։
Բաժանումը, որն առանց լոգարիթմների օգնությամբ բավականին դժվար է, քան արտադրյալը, կատարվում է նույն ալգորիթմով, միայն լոգարիթմների գումարը փոխարինելով նրանց տարբերությամբ։ Նմանապես, պարզեցվել են աստիճանի բարձրացումը և արմատի հանումը։
Լոգարիթմի հիմքի փոխարինումը
խմբագրելԼոգարիթմը որի հիմքը -ն է, կարելի է փոխակերպել [5]մեկ այլ հիմքի լոգարիթմի հետևյալ բանաձով՝
Հետևանք (երբ ) - հիմքի և լոգարիթմվող արտահայտության տեղափոխություն՝
Գործակիցը հիմքի փոխարինման բանաձևում կոչվում է անցման մոդուլ մի հիմքից մյուսին[7]։
Անհավասարություն
խմբագրելլոգարիթմի արժեքը դրական է այն և միայն այն դեպքում, երբ թվերը գտնվում են մեկի միևնույն կողմում (այսինքն կամ երկուսն էլ մեծ են մեկից, կամ երկուսն էլ փոքր են մեկից)։ Իսկ եթե -ն և -ն ընկած են մեկի տարբեր կողմերում, ապա լոգարիթմը բացասական է։
Դրական թվերի համար ցանկացած անհավասարություն կարելի է լոգարիթմել։ Այդ դեպքում եթե լոգարիթմի հիմքը մեծ է մեկից, ապա անհավասարության նշանը պահպանվում է, իսկ եթե հիմքը փոքր է մեկից, անհավասարության նշանը փոխարինվում է հակառակին։
Այլ հավասարություններ և հատկություններ
խմբագրելԵթե լոգարիթմի հիմքը և լոգարիթմվող արտահայտությունը պարունակում են աստիճանի բարձրացման արտահայտություն, նրանց համար կարելի է օգտագործել հետևյալ պարզ հավասարությունը՝
Այս հավասարությունը միանգամից ստացվում է, եթե լոգարիթմի ձախ մասում հիմքը փոխարինում ենք հիմքով, վերևում նշված հիմքի փոխարինման բանաձևով։ Հետևանք՝
Եվս մեկ օգտակար հավասարում՝
Նրա ապացուցման համար կարելի է տեսնել, որ լոգարիթմի ձախ և աջ մասերը հիմքով համընկնում են (հավասար են ), համաձայն լոգարիթմական հավասարության հետևում է, որ հավասարության ձախ և աջ մասերը իրար հավասար են։
Լոգարիթմանական ֆունկցիա
խմբագրելՀիմնական բնութագրերը
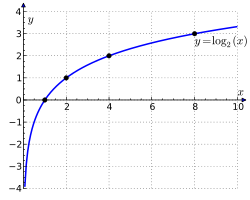
խմբագրելԵթե դիտարկենք լոգարիթմվող թիվը՝ որպես փոփոխական, մենք կստանանք լոգարիթմական ֆունկցիան։ Այն որոշված է -ի համար։ Արժեքների տիրույթն է՝ ։ Այս կորը հաճախ անվանում են լոգարիթմական[8]։ Լոգարիթմի հիմքի փոխարինման բանաձևից երևում է, որ տարբեր հիմքերով լոգարիթմական ֆունկցիայի գրաֆիկը մեծ է մեկից և մեկը մյուսից տարբերվում են միայն -ի առանցքի նկատմամբ միայն մասշտաբով, իսկ 1-ից փոքր հիմքով գրաֆիկները հանդիսանում են նրանց հայելային արտապատկերումները հորիզոնական առանցքի նկատմամբ։
Սահմանումից հետևում է, որ լոգարիթմական կապը հանդիսանում է ցուցչային ֆունկցիայի համար հակադարձ ֆունկցիա, հետևաբար նրանց գրաֆիկները սիմետրիկ են առաջին և երրորդ քարորդների կիսորդի նկատմամբ (տես նկարը)։ Ինչպես և ցուցչային ֆունկցիան, այնպես էլ լոգարիթմական ֆունկցիան դասվում են տրանսցենդենտ ֆունկցիաների կատեգորիային։
Ֆունկցիան հանդիսանում է խիստ աճող -ի դեպքում (տես հաջորդ գրաֆիկը) և խիստ նվազող -ի դեպքում։ Ցանկացած լոգարիթմական ֆունկցիայի գրաֆիկը անցնում է կետով։ Ֆունկցիան անընդհատ է և անսահամանափակ դիֆերենցվող է իր որոշման ամբողջ տիրույթում։
Օրդինատների առանցքը ( ) հանդիսանում է ձախ ասիմպտոտիկ ուղղահայաց, քանի որ՝
, երբ ;
, երբ ։
Լոգարիթմական ֆունկցիայի ածանցյալը հավասար է՝
Հանրահաշվի տեսանկյունից լոգարիթմական ֆունկցիան (միակ հնարավոր) իզոմորֆիզմ է դրական իրական թվերի մուլտիպլիկտիվ խմբի և բոլոր իրական թվերի ադիտիվ խմբի համար։ Այլ բառերով, լոգարիթմական ֆունկցիան հանդիսանում է հետևյալ ֆունկցիոնալ հավասարման միակ անընդհատ լուծումը՝
Պատմական ակնարկ
խմբագրելՆախադրյալներ
խմբագրելԼոգարիթմների գաղափարական աղբյուրը և կիրառման խթանը եղել է այն փաստը (հայտնի է եղել դեռ Արքիմեդեսին[9]), որ նույն հիմքով աստիճանները բազմապատկելիս դրանց ցուցիչները գումարվում են[10]. : 13-րդ դարի հնդիկ մաթեմատիկոս Վիրասենան, ուսումնասիրելով աստիճանային կախվածությունները, հրապարակել է 2, 3, 4 հիմքերի համար ամբողջ թվերով ցուցիչների (այսինքն, ըստ էության, լոգարիթմների) աղյուսակը[11]։
Վճռական քայլն արվել է միջնադարյան Եվրոպայում։ XVI դարում բարդ հաշվարկների անհրաժեշտությունը արագորեն մեծացել է, և դժվարությունների մեծ մասը կապված էր բազմանիշ թվերի բազմապատկման և բաժանման, ինչպես նաև արմատ հանելու հետ։ Դարավերջին մի քանի մաթեմատիկոսներ գրեթե միաժամանակ հանդես են եկել հետևյալ գաղափարով. ժամանակատար բազմապատկումը փոխարինել պարզ գումարումով՝ հատուկ աղյուսակների միջոցով հակադրելով երկրաչափական և թվաբանական պրոգրեսիաները, ընդ որում՝ երկրաչափականը կլինի ելակետայինը[9]։ Այնուհետև բաժանումը ինքնաբերաբար փոխարինվում է շատ ավելի պարզ և հուսալի հանումով, և դրանով պարզեցվում են նաև աստիճանի բարձրացումն ու արմատ հանելը։
Առաջին անգամ այս գաղափարը հրատարակվել է Մայքլ Շտիֆելի «Arithmetica integra» (1544) գրքում, որը, սակայն, լուրջ ջանքեր չի գործադրել իր գաղափարի գործնական իրականացման համար[12][13]։ Շտիֆելի հիմնական արժանիքը ամբողջ թվային ցուցիչներից կամայական ռացիոնալի անցումն է[14] (այս ուղղությամբ առաջին քայլերը կատարել են Նիկոլայ Օրեսմը XIV դարում և Նիկոլա Շյուկեն XV դարում)։
Ջոն Նեփյերը և նրա «լոգարիթմների զարմանալի աղյուսակը»
խմբագրել1614 թվականին շոտլանդացի սիրողական մաթեմատիկոս Ջոն Նեփյերը հրատարակել է լատիներեն աշխատություն «Լոգարիթմների զարմանալի աղյուսակի նկարագրությունը» (լատին․՝ Mirifici Logarithmorum Canonis Descriptio) վերնագրով։ Այն ներկայացնում էր լոգարիթմների և դրանց հատկությունների համառոտ նկարագրությունը, ինչպես նաև սինուսների, կոսինուսների և տանգենսների լոգարիթմների ութանիշ աղյուսակներ՝ 1' քայլով։ Նեփյերի առաջարկած լոգարիթմ տերմինը հաստատվել է գիտության մեջ։ Նեփյերն ուրվագծել է լոգարիթմների տեսությունը իր մյուս գրքում՝ «Լոգարիթմների զարմանալի աղյուսակի կառուցումը»(լատին․՝ Mirifici Logarithmorum Canonis Constructio), որը հետմահու հրատարակվել է 1619 թվականին նրա որդու՝ Ռոբերտի կողմից։
Դատելով փաստաթղթերից՝ Նեփյերը լոգարիթմի տեխնիկան յուրացրել է մինչև 1594 թվականը[15]։ Նրա զարգացման անմիջական նպատակն է եղել հեշտացնել բարդ աստղագիտական հաշվարկները[16], այդ իսկ պատճառով աղյուսակներում ներառվել են միայն եռանկյունաչափական ֆունկցիաների լոգարիթմները։
Ֆունկցիայի հասկացությունն այդ ժամանակ դեռ գոյություն չի ունեցել, և Նեփյերը կինեմատիկորեն է որոշել լոգարիթմը՝ համեմատելով համաչափ և լոգարիթմական-դանդաղ շարժումը. օրինակ՝ նա սահմանել է սինուսի լոգարիթմը հետևյալ կերպ[17].
Տրված սինուսի լոգարիթմը այն թիվն է, որը միշտ թվաբանորեն աճել է նույն արագությամբ, երբ լրիվ սինուսը սկսել է երկրաչափորեն նվազել։
Ժամանակակից նշումով Նեփյերի կինեմատիկական մոդելը կարող է ներկայացվել դիֆերենցիալ հավասարմամբ[18].
- ,
որտեղ M-ը մասշտաբային բազմապատկիչն է, որը ներդրվել է արժեքն անհրաժեշտ թվանշաններով ամբողջ թիվ դարձնելու համար (տասնորդական թվերն այն ժամանակ դեռ լայնորեն չեն կիրառվել)։ Նեփյերը վերցրել է M = 10 000 000։
Ավելի ստույգ՝ Նեփյերը աղյուսակավորել է ոչ այն ֆունկցիան, որն այժմ կոչվում է լոգարիթմ։ Եթե սահմանենք նրա ֆունկցիան, ապա այն կապված է բնական լոգարիթմի հետ հետևյալ կերպ[18].
Ակնհայտ է, որ , այսինքն՝ «լրիվ սինուսի» լոգարիթմը (համապատասխանում է 90 °) զրոյական է. սա այն է, ինչ Նեփյերը փնտրում էր իր սահմանմամբ։ Նա նաև ցանկանում էր, որ բոլոր լոգարիթմները դրական լինեն. հեշտ է ստուգել, որ պայմանը բավարարված է դեպքում։
Նեփյերի լոգարիթմի հիմնական հատկությունն է՝ եթե մեծությունները կազմում են երկրաչափական պրոգրեսիա, ապա դրանց լոգարիթմները կազմում են թվաբանական պրոգրեսիա։
Այնուամենայնիվ, Նեփյերի ֆունկցիայի լոգարիթմի կանոնները տարբերվում էին ժամանակակից լոգարիթմի կանոններից, ինչպիսիք են.
Հետագա զարգացում
խմբագրելԻնչպես շուտով պարզվել է, ալգորիթմի սխալի պատճառով Նեփյերի աղյուսակի բոլոր արժեքները վեցերորդ թվանշանից հետո սխալ թվեր էին պարունակում[19]։ Այնուամենայնիվ, դա չի խանգարել, որ հաշվարկի նոր մեթոդը լայն ժողովրդականություն ձեռք բերի, և շատ եվրոպացի մաթեմատիկոսներ զբաղվել են լոգարիթմական աղյուսակների կազմումով։ Կեպլերը խանդավառությամբ է խոսել Նեփյերի մասին 1620 թվականին հրատարակված իր աստղագիտական գրքում (չիմանալով, որ լոգարիթմների գյուտարարն արդեն մահացել է)։ 1624 թվականին Կեպլերը հրատարակել է լոգարիթմական աղյուսակների իր տարբերակը (լատ.՝ Chilias Logarithmorum ad totidem numeros rotundos)[20]։ Լոգարիթմների օգտագործումը Կեպլերին թույլ է տվել համեմատաբար արագ ավարտել երկար տարիների աշխատանքը Ռուդոլֆյան աղյուսակների կազմման վրա, որոնք ամրապնդել են արևակենտրոն աստղագիտության հաջողությունը։
Նեփյերի գրքի լույս տենելուց մի քանի տարի անց հայտնվել են լոգարիթմական աղյուսակներ՝ օգտագործելով լոգարիթմի ավելի ժամանակակից ըմբռնումը։ Լոնդոնում պրոֆեսոր Հենրի Բրիգսը հրապարակել է տասնորդական լոգարիթմների 14 նիշանոց աղյուսակներ (1617), ընդ որում՝ ոչ թե եռանկյունաչափական ֆունկցիաների, այլ մինչև 1000 կամայական ամբողջ թվերի համար (7 տարի անց Բրիգսը թվերի թիվը հասցրել է 20000-ի)։ 1619 թվականին Լոնդոնում մաթեմատիկայի ուսուցիչ Ջոն Սփայդելը (անգլ.՝ John Speidell) վերահրատարակել է Նեփյերի լոգարիթմական աղյուսակները, ուղղել և լրացրել այնպես, որ դրանք իրականում դարձել են բնական լոգարիթմների աղյուսակներ։ Սփայդելն ունեցել է նաև մինչև 1000 թվերի լոգարիթմները (ընդ որում՝ միավորի լոգարիթմը, ինչպես Բրիգսի մոտ, հավասար էր զրոյի), չնայած Սփայդելը պահպանել է մասշտաբավորումը մինչև ամբողջ թվեր[21][22]։
Շուտով պարզ է դարձել, որ լոգարիթմների տեղը մաթեմատիկայում չի սահմանափակվում հաշվողական հարմարություններով։ 1629 թվականին բելգիացի մաթեմատիկոս Գրեգուար դը Սեն Վինսենը ցույց է տվել, որ -ի հիպերբոլի տակ գտնվող մակերեսը փոխվում է ըստ լոգարիթմական օրենքի[23]։ 1668 թվականին գերմանացի մաթեմատիկոս Նիկոլաս Մերկատորը (Կաուֆման) իր «Logarithmotechnia » գրքում հրատարակել է լոգարիթմի ընդլայնումը անսահման շարքում[24]։ Շատ պատմաբանների կարծիքով, լոգարիթմների հայտնվելը մեծ ազդեցություն է ունեցել մաթեմատիկական բազմաթիվ հասկացությունների վրա, այդ թվում.
- Իռացիոնալ և տրանսցենդենտ թվերի ընդհանուր հասկացության ձևավորում և ճանաչում[25],
- Ցուցչային ֆունկցիայի և թվային ֆունկցիայի ընդհանուր հասկացության, Էյլերի թվի ի հայտ գալը, տարբերությունների հավասարումների տեսության մշակումը[26],
- Անվերջ շարքերով աշխատանքի սկիզբը[24],
- Տարբեր տեսակների դիֆերենցիալ հավասարումների լուծման ընդհանուր մեթոդներ,
- Ճշգրիտ լոգարիթմական աղյուսակների հաշվարկման համար անհրաժեշտ թվային մեթոդների տեսության զգալի զարգացում։
Մինչև 19-րդ դարի վերջը լոգարիթմի ընդհանուր ընդունված գրելաձև չի եղել. a հիմքը նշվել է կամ log սիմվոլից ձախ ու վերև, կամ դրա վերևում։ Ի վերջո, մաթեմատիկոսները եկել են այն եզրակացության, որ հիմքի համար ամենահարմար տեղը գծից ներքև է՝ log սիմվոլից հետո՝ : Լոգարիթմի ամենատարածված ձևերի հակիրճ նշանակումները՝ տասնորդական և բնական լոգարիթմների համար, հայտնվել են շատ ավելի վաղ միանգամից մի քանի հեղինակների կողմից և վերջնականապես հաստատվել են նույնպես 19-րդ դարի վերջին[27]։
Լոգարիթմի ժամանակակից ըմբռնումը՝ որպես աստիճանի բարձրացման հակադիր գործողություն, առաջին անգամ հայտնվել է Ջոն Վալլիսի (1685) և Յոհան Բեռնուլիի (1694) մոտ և վերջնական հատատվել է Էյլերի կողմից։ Իր «Անվերջ փոքրերի վերլուծության ներածություն» (1748) գրքում Էյլերը տվել է ինչպես ցուցչային, այնպես էլ լոգարիթմական ֆունկցիաների ժամանակակից սահմանումներ, դրանք ընդլայնել է աստիճանային շարքերում և հատուկ նշել է բնական լոգարիթմի դերը[28]։ Էյլերին է պատկանում նաև լոգարիթմական ֆունկցիան կոմպլեքս տիրույթում ընդլայնելու արժանիքը։
Լոգարիթմի ընդլայնում դեպի կոմպլեքս տիրույթ
խմբագրելԼոգարիթմները կոմպլեքս թվերի վրա ընդլայնելու առաջին փորձերն արվել են 17-18-րդ դարերի վերջում՝ Լայբնիցի և Յոհան Բեռնուլիի կողմից, բայց նրանք չեն կարողացել ստեղծել ամբողջական տեսություն առաջին հերթին այն պատճառով, որ լոգարիթմի գաղափարը դեռևս հստակ չէր սահմանված[29]։ Այս թեմայի շուրջ քննարկումները սկզբում ծավալվել են Լայբնիցի և Բեռնուլիի, իսկ 18-րդ դարի կեսերին՝ դ'Ալմբերի և Էյլերի միջև։ Բեռնուլին և դ'Ալեմբերը հավատում էին, որ , մինչդեռ Լայբնիցը պնդում էր, որ բացասական թվի լոգարիթմը երևակայական թիվ է[29]։ Բացասական և կոմպլեքս թվերի լոգարիթմների ամբողջական տեսությունը հրապարակվել է Էյլերի կողմից 1747-1751 թվականներին և ըստ էության չի տարբերվում ժամանակակիցից[30]։ Թեև վեճը շարունակվել է (դ'Ալեմբերը պաշտպանել է իր տեսակետը և մանրամասն փաստարկել այն իր «Հանրագիտարանի» հոդվածում և այլ աշխատություններում), 18-րդ դարի վերջում Էյլերի մոտեցումը համընդհանուր ընդունելություն է գտել։
19-րդ դարում՝ կոմպլեքս անալիզի զարգացման հետ մեկտեղ, բարդ լոգարիթմի ուսումնասիրությունը խթանել է նոր հայտնագործությունների կատարումը։ Կառլ Գաուսը 1811 թվականին մշակել է լոգարիթմական ֆունկցիայի բազմարժեքության ամբողջական տեսությունը[31], որը սահմանվում է որպես -ի ինտեգրալ։ Բեռնարդ Ռիմանը, հենվելով այս և նմանատիպ ֆունկցիաների մասին արդեն հայտնի փաստերի վրա, կառուցել է Ռիմանի մակերևույթների ընդհանուր տեսությունը։
Կոնֆորմ արտապատկերումների տեսության զարգացումը ցույց է տվել, որ քարտեզագրության մեջ Մերկատորի պրոյեկցիան, որն առաջացել է նույնիսկ մինչև լոգարիթմների հայտնաբերումը (1550 թվականին), կարելի է բնութագրել որպես կոմպլեքս լոգարիթմ[32]։
Գործնական կիրառություններ
խմբագրելԼոգարիթմական հարաբերությունները գիտության և բնության մեջ
խմբագրելԼոգարիթմական ֆունկցիաները չափազանց տարածված են թե՛ մաթեմատիկայում, թե՛ բնական գիտությունների մեջ։ Հաճախ լոգարիթմները հայտնվում են այնտեղ, որտեղ տեղի է ունենում ինքնանմանություն, այսինքն՝ ինչ-որ առարկա հետևողականորեն վերարտադրվում է փոքրացված կամ մեծացված մասշտաբով, օրինակ՝ ռեկուրսիվ ալգորիթմները, ֆրակտալները կամ կակղամորթերի խեցիները։
Թվերի տեսություն
խմբագրելՊարզ թվերի ասիմպտոտ բաշխումը ենթարկվում է պարզ օրենքների[33]։
- 1-ից մինչև միջակայքում պարզ թվերի քանակը մոտավորապես հավասար է ,
- k-րդ պարզ թիվը մոտավորապես հավասար է ,
Ավելի ճշգրիտ գնահատումներն օգտագործում են ինտեգրալ լոգարիթմը։
Հաճախ խնդիր է առաջանում գնահատել շատ մեծ թիվ, օրինակ՝ մեծ համարով Մերսենի թիվը կամ ֆակտորիալը։ Դրա համար հարմար կլինի թիվը մոտավորապես գրել էքսպոնենտալ ձևաչափով, այսինքն՝ մանտիսի և տասնորդական կարգի տեսքով։
Խնդիրը հեշտությամբ լուծվում է լոգարիթմների օգտագործմամբ։ Որպես օրինակ դիտարկենք Մերսենի 44-րդ թիվը .
Հետևաբար, արդյունքի մանտիսը հավասար է ։ Արդյունքում կստանանք.
Մաթեմատիկական անալիզ
խմբագրելԼոգարիթմները հաճախ կիրառվում են ինտեգրալներ գտնելու և դիֆերենցիալ հավասարումների լուծման ժամանակ, օրինակ՝
Հավանականությունների տեսություն և վիճակագրություն
խմբագրելՎիճակագրության և հավանականությունների տեսության մեջ լոգարիթմը ներառված է գործնականում կարևոր հավանականության բաշխումների շարքում։ Օրինակ՝ լոգարիթմական բաշխումն[34] օգտագործվում է գենետիկայում և ֆիզիկայում։ Լոգնորմալ բաշխումը հաճախ տեղի է ունենում այն իրավիճակներում, երբ հետազոտվող մեծությունը մի քանի անկախ դրական պատահական փոփոխականների արտադրյալ է[35]։
Բենֆորդի օրենքը («առաջին նիշի օրենք») նկարագրում է իրական մեծությունները չափելիս որոշակի առաջին նշանակալի թվանշանի առաջացման հավանականությունը։
Անհայտ պարամետրը գնահատելու համար լայնորեն կիրառվում են առավելագույն ճշմարտանմանության մեթոդը և դրա հետ կապված ճշմարտանմանության լոգարիթմական ֆունկցիան[36]։
Ինֆորմատիկա և հաշվողական մաթեմատիկա
խմբագրելԻնֆորմատիկա – տեղեկատվության չափման միավոր (բիթ)։ Օրինակ՝ համակարգչում բնական թիվը (համակարգչի համար սովորական երկուական ձևաչափով) պահպանելու համար անհրաժեշտ է բիթ։
Տեղեկատվական էնտրոպիան տեղեկատվության քանակի չափումն է։
«Բաժանիր և տիրիր» սկզբունքի վրա հիմնված ռեկուրսիվ ալգորիթմների ասիմպտոտիկ բարդության գնահատում[37], ինչպիսիք են արագ տեսակավորումը, Ֆուրիեի արագ փոխակերպումը և այլն։
Սովորաբար թվային արժեքները պահվում են համակարգչի կամ մասնագիտացված պրոցեսորի հիշողության մեջ՝ լողացող ստորակետի ձևաչափով։ Եթե, այնուամենայնիվ, տվյալների խմբի համար գումարումը և հանումը հազվադեպ են կատարվում, իսկ բազմապատկումը, բաժանումը, աստիճանի բարձրացումը և արմատ հանելը շատ ավելի հաճախ, ապա իմաստ ունի դիտարկել այդպիսի տվյալները լոգարիթմական ձևաչափով պահպանելու հնարավորությունը։ Այս դեպքում թվի փոխարեն պահվում է նրա մոդուլի լոգարիթմը և նշանը, և լոգարիթմի հատկությունների շնորհիվ հաշվարկների արագությունը զգալիորեն մեծանում է[38]։ Պահպանման լոգարիթմական ձևաչափը օգտագործվել է մի քանի համակարգերում, որտեղ ապացուցել է նրա արդյունավետությունը[39][40]։
Մեխանիկա և ֆիզիկա
խմբագրելԲոլցմանի սկզբունքը վիճակագրական թերմոդինամիկայի մեջ թերմոդինամիկական համակարգի վիճակի կարևորագույն գործառույթներից է, որը բնութագրում է դրա աստիճանը։
Հրթիռի արագությունը հաշվարկվելու համար օգտագործվում է Ցիոլկովսկու բանաձևը։
Քիմիա և ֆիզիկական քիմիա
խմբագրելՆեռնստի հավասարումն արտահայտում է համակարգի Օքսիդա-վերականգնման պոտենցիալի և էլեկտրաքիմիական հավասարման մեջ ներառված նյութերի ակտիվության, ինչպես նաև օքսիդա-վերականգնման զույգերի ստանդարտ էլեկտրոդային պոտենցիալների կապը։
Լոգարիթմը օգտագործվում է այնպիսի մեծությունների սահմանումներում, ինչպիսիք են ավտոպրոտոլիզի հաստատունի ինդեքսը (մոլեկուլի ինքնաիոնացում) և ջրածնային ինդեքսը (լուծույթի թթվայնությունը)։
Հոգեբանություն և ֆիզիոլոգիա
խմբագրելՇատ երևույթների մարդկային ընկալումը հարմար է նկարագրել լոգարիթմական օրենքով։
Վեբեր Ֆեխների օրենքը էմպիրիկ հոգեֆիզիոլոգիական օրենք է, ըստ որի՝ զգայության ինտենսիվությունը համաչափ է գրգռիչի ինտենսիվության լոգարիթմին, օրինակ՝ ձայնի բարձրության, լույսի պայծառության[41][42]։
Ընտրության առկայության դեպքում որոշում կայացնելու ժամանակը կարելի է գնահատել Հիկի օրենքի համաձայն[43]։
Կենսաբանություն
խմբագրելՄի շարք կենսաբանական ձևեր նման են լոգարիթմական պարույրի[44]՝ կորի, որի դեպքում յուրաքանչյուր կետով անցնող շոշափողը նուն կետով անցնող շառավիղ-վեկտորի հետ կազմում է անույն այնկյունը, այսինքն՝ շառավիղի աճը շրջանագծի միավորի երկարության համար հաստատուն է։
-
Նաուտիլուսի խեցի -
Արևածաղկի սերմերի դասավորությունը -
Ռոմանեսկո (կաղամբ)
Երաժշտության տեսություն
խմբագրելՈրոշելու համար, թե քանի մասի պետք է բաժանել օկտավան, պահանջվում է գտնել ռացիոնալ մոտարկումը համար։ Եթե այդ թիվը դարձնենք շղթայական կոտորակ, ապա երրորդ կոտորակը (7/12) թույլ է տալիս հիմնավորել օկտավայի դասական բաժանումը 12 կիսատոնների[45]։
Այլ
խմբագրելՕլիմպիական համակարգում խաղերի պտույտների թիվը հավասար է մրցույթի մասնակիցների թվի երկուական լոգարիթմին՝ կլորացված մինչև մոտակա մեծ ամբողջ թիվը[46]։
Լոգարիթմական քանոն
խմբագրել1620-ական թվականներին Էդմունդ Ուինգեյթը և Ուիլյամ Օտրեդը հայտնագործել են առաջին լոգարիթմական քանոնը, որը մինչև գրպանի հաշվիչների հայտնվելը ծառայել է որպես ինժեների անփոխարինելի հաշվարկային գործիք[47]։ Այս կոմպակտ գործիքի օգնությամբ կարելի է արագ կատարել բոլոր հանրահաշվական գործողությունները, այդ թվում՝ եռանկյունաչափական ֆունկցիաների մասնակցությամբ[48]։ Հաշվարկների ճշգրտությունը մոտ 3 թվանշան է։
Ծանոթագրություններ
խմբագրել- ↑ Краткий словарь иностранных слов. М.: Русский язык, 1984.
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, էջ 186.
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, էջ 184-186.
- ↑ Швецов К. И., Бевз Г. П. Справочник по элементарной математике. Арифметика, алгебра. Киев: Наукова Думка, 1966. §40. Исторические сведения о логарифмах и логарифмической линейке.
- ↑ 5,0 5,1 Корн Г., Корн Т. Справочник по математике, 1973, էջ 34.
- ↑ Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 229.
- ↑ Элементарная математика, 1976, էջ 93.
- ↑ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ 9,0 9,1 Успенский Я. В. Очерк истории логарифмов, 1923, էջ 9
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, էջ 206
- ↑ Gupta, R. C. (2000), «History of Mathematics in India», in Hoiberg, Dale; Ramchandani (eds.), Students' Britannica India: Select essays, New Delhi: Popular Prakashan, էջ 329, Արխիվացված է օրիգինալից 2018 թ․ մարտի 17-ին, Վերցված է 2022 թ․ դեկտեմբերի 14-ին
{{citation}}:|editor3-first=missing|editor3-last=(օգնություն) - ↑ История математики, том II, 1970, էջ 54—55
- ↑ Vivian Shaw Groza, Susanne M. Shelley (1972), Precalculus mathematics, New York: Holt, Rinehart, Winston, էջ 182, ISBN 978-0-03-077670-0
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, էջ 210
- ↑ Успенский Я. В. Очерк истории логарифмов, 1923, էջ 13
- ↑ История математики, том II, 1970, էջ 56
- ↑ E. E. Swartzlander and A. G. Alexopoulos The Sign/Logarithm Number System(անգլ.) // IEEE Transactions on Computers : journal. — 1975. — Т. C—24. — № 12. — С. 1238—1242. —
- ↑ 18,0 18,1 История математики, том II, 1970, էջ 59
- ↑ История математики, том II, 1970, էջ 61
- ↑ Успенский Я. В. Очерк истории логарифмов, 1923, էջ 39
- ↑ История математики, том II, 1970, էջ 63
- ↑ Charles Hutton. Mathematical Tables. Արխիվացված 2016-09-11 Wayback Machine London, 1811, p. 30.
- ↑ История математики, том II, 1970, էջ 133
- ↑ 24,0 24,1 Успенский Я. В. Очерк истории логарифмов, 1923, էջ 52
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, էջ 51, 286, 352
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей, 1987, էջ 213, 217
- ↑ R.C Ismail and J.N Coleman ROM-less LNS (und) // 2011 20th IEEE Symposium on Computer Arithmetic (ARITH). — 2011. — С. 43—51. —
- ↑ Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 25.
- ↑ 29,0 29,1 История математики, том III, 1972, էջ 325-328
- ↑ Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 27, 230—231.
- ↑ Математика XIX века. Том II: Геометрия. Теория аналитических функций, 1981, էջ 122-123
- ↑ Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. II. Геометрия. — С. 159—161. — 416 с.
- ↑ Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2
- ↑ Weisstein, Eric W. «Log-Series Distribution» (անգլերեն). MathWorld. Արխիվացված օրիգինալից 2012 թ․ մայիսի 11-ին. Վերցված է 2012 թ․ ապրիլի 26-ին.
- ↑ Логарифмически нормальное распределение // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Максимального правдоподобия метод // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Harel, David; Feldman, Yishai A. Algorithmics: the spirit of computing. — New York: Addison-Wesley, 2004. — P. 143. — ISBN 978-0-321-11784-7
- ↑ N. G. Kingsburg, P. J. W. Rayner Digital filtering using logarithmic arithmetic(անգլ.) // Electronics Letters : journal. — 1971. — Т. 7. — С. 55.
- ↑ R. C. Ismail and J. N. Coleman ROM-less LNS (und) // 2011 20th IEEE Symposium on Computer Arithmetic (ARITH). — 2011. — С. 43—51. —
- ↑ Haohuan Fu, Oskar Mencer, Wayne Luk Comparing Floating-point and Logarithmic Number Representations for Reconfigurable Acceleration(անգլ.) // IEEE Conference on Field Programmable Technology : journal. — 2006. — С. 337. —
- ↑ Головин С. Ю. «ЗАКОН ВЕБЕРА-ФЕХНЕРА // Словарь практического психолога». Արխիվացված օրիգինալից 2012 թ․ մայիսի 27-ին. Վերցված է 2012 թ․ ապրիլի 17-ին.
- ↑ Ирина Алдошина. Основы психоакустики // Звукорежиссёр. — 1999. — В. 6. Архивировано из первоисточника 24 Ապրիլի 2012.
- ↑ «Закон Фиттса // Психологическая энциклопедия». Արխիվացված օրիգինալից 2012 թ․ մայիսի 27-ին. Վերցված է 2012 թ․ ապրիլի 17-ին.
- ↑ Логарифмическая спираль // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров. — М.: Советская энциклопедия, 1988. — С. 328. — 847 с. — ISBN 5-85270-278-1
- ↑ Шилов Г. Е. Простая гамма. Устройство музыкальной шкалы. Արխիվացված 2014-02-22 Wayback Machine М.: Физматгиз, 1963. 20 с. Серия «Популярные лекции по математике», выпуск 37.
- ↑ Харин А. А. Организация и проведение соревнований. Методическое пособие. — Ижевск: УдГУ, 2011. — С. 27.
- ↑ История математики, том II, 1970, էջ 65-66
- ↑ Березин С. И. Счётная логарифмическая линейка. — М.: Машиностроение, 1968.
| Այս հոդվածի կամ նրա բաժնի որոշակի հատվածի սկզբնական կամ ներկայիս տարբերակը վերցված է Քրիեյթիվ Քոմմոնս Նշում–Համանման տարածում 3.0 (Creative Commons BY-SA 3.0) ազատ թույլատրագրով թողարկված Հայկական սովետական հանրագիտարանից (հ․ 4, էջ 650)։ |












