Քառակուսային բանաձև
Քառակուսային բանաձև, բանաձև է տարրական հանրահաշվում, որով կարող ենք քառակուսային հավասարումներ լուծել։ Քառակուսային հավասարումներ լուծելու այլ եղանակներ կան, ինչպես, օրինակ՝ ֆակտորիզացիան (ուղղակի ֆակտորիզացիա, խմբավորում), քառակուսին լրացնելը, գրաֆիկ գծելը և այլն[1]։
Տրված է քառակուսային հավասարում՝ իր ընդհանուր տեսքով , որտեղ ֊ը անհայտն է, ֊ն, ֊ն և ֊ն՝ հաստատուններ են, այնպես, որ ։ Քառակուսային բանաձևը հետևյալն է․
Բանաձևի պլյուս֊մինուսի նշանը՝ , ցույց է տալիս, որ քառակուսային հավասարումը երկու արմատ ունի[2]։ Առանձին գրելու դեպքում կստանանք հետևյալ երկու բանաձևերը․
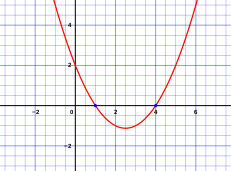
Երկու արժեքներից յուրաքանչյուրը կոչվում է քառակուսային հավասարման արմատ (կամ՝ զրո)։ Երկրաչափորեն՝ արմատներն ֊ի այն արժեքներն են ներկայացնում, որոնցում հավասարմամբ սահմանված ցանկացած պարաբոլ կհատի ֊երի առանցքը[3]։
Քառակուսային հավասարումը կարող է նաև օգտակար լինել պարաբոլի համաչափության առանցքները[4] և քառակուսային հավասարման իրական զրոների քանակը[5] գտնելուն։
Համարժեք ձևակերպումներ
խմբագրելՔառակուսային հավասարումը կարելի է գրել նաև հետևյալ տեսքով․
որը կարող ենք պարզեցնել․
Բանաձևի այս տեսքը հարմար է կոմպլեքս արմատների առկայության դեպքում․ քառակուսի արմատից դուրս հատվածը կներկայացնի կոմպլեքս արմատի իրական մասը, իսկ քառակուսի արմատի տակ գտնվող արտահայտությունը՝ կեղծ մասը։ Քառակուսի արմատի տակ գտնվող արտահայտությունը դիսկրիմինանտ է։
Մյուլլերի մեթոդը
խմբագրելՊակաս հայտնի քառակուսային բանաձև է, որը օգտագործվում է Մյուլլերի մեթոդում, ինչպես նաև հայտնվում է Վիետի թեորեմում։ Տալիս է նույն արմատները՝ հետևյալ հավասարմամբ․
Ձևակերպումներ՝ այլընտրանքային պարամետրիզացիայի հիման վրա
խմբագրելՔառակուսային հավասարման ստանդարտ պարամերիզացիան հետևյալն է․ ։ Որոշ աղբյուրներ՝ հատկապես հին աղբյուրները, օգտագործում են հետևյալ այլընտրանքային ձևակերպումը․ , որտեղ [6], կամ , որտեղ [7]:
Այլընտրանքային ձևակերպումների համապատասխան բանաձևերը փոքր֊ինչ տարբերվող տեսք ունեն, բայց բովանդակայնորեն համարժեք են ստանդարտին։
Բանաձևի ստացումը
խմբագրելԳիտական գրականության մեջ քառակուսային բանաձև ստանալու շատ մեթոդներ կան նկարագրված։ Ամենատարածվածը քառակուսու լրացման տեխնիկան է[8][9][10][11]։ Այլընտրանքային մեթոդները երբեմն ավելի պարզ են, քան քառակուսին լրացնելը, և կարող են օգտակար լինել մաթեմատիկայի այլ ոլորտների հետ կապեր տեսնելուն։
Քառակուսին լրացնելով
խմբագրելՍտանդարտ մեթոդ
խմբագրելԲաժանեք քառակուսային հավասարումը ֊ով, ինչը հնարավոր է, քանի որ երաշխավորված է սահմանմամբ․
Երկու կողմից հանեք ՝ ստանալով․
Քառակուսային հավասարումն այժմ այն տեսքով է, որով հնարավոր է լրացնել քառակուսին։ Իրականում, հավասարման երկու կողմերին պարզապես հաստատուն ավելացնելով՝ կարող ենք ձախ կողմում ամբողջական քառակուսի ստանալ․
որից ստանում ենք․
Համապատասխանաբար, աջ կողմում անդամները վերադասավորելով և ընդհանուր հայտարարի բերելով կարող ենք ստանալ․
Քառակուսին լրացված է։ Երկու կողմից քառակուսի արմատ հանելով ստանում ենք․
Արդեն նպատակահարմար է անհայտները հավաքել հավասարման մի կողմում, հայտնիների՝ մյուս կողմում, վերջնական բանաձևը ստանալու համար․
Բանաձևի ստացման շատ այլընտրաքային ճանապարհներ կան՝ չնչին տարբերություններով․ հիմնական տարբերությունը -ի հետ արվող փոփոխություններն են։
Երկրորդ մեթոդ
խմբագրելՎերջին մի քանի տասնամյակում հրատարակվաշ հանրահաշվական աշխատությունների մեծամասնությունը քառակուսին լրացնելու համար հետևյալ հաջորդականությունն է առաջարկում․
- Բաժանել հավասարման երկու կողմը -ով՝ միավոր գործակցով առաջատար անդամով բազմանդամ ստանալու համար։
- Վերախմբավորել։
- Հավասարման երկու կողմին ավելացնել։
- Երկու կողմից քառակուսի արմատ հանել։
- Մեկուսացնել ֊ը։
Քառակուսին լրացնելը երբեմն հնարավոր է իրականացնել ավելի պարզ ու կարճ հաջորդականությամբ․[12]
- Բազմապատկել յուրաքանչյուր կողմը ֊ով
- Վերադասավորել։
- Երկու կողմին ավելացնել՝ քառակուսին լրացնելու համար։
- Երկու կողմից քառակուսի արմատ հանել։
- Մեկուսացել ֊ը։
Այսպիսով, քառակուսային բանաձևը կարող ենք ստանալ հետևյալ հաջորդականության արդյունքում․
Քառակուսային բանաձևի այս ստացման եղանակը բավականին հին է, և հայտնի էր Հնդկաստանում արդեն առնվազն 1025 թվականին[13]։ Ի հակադրությունտ ստանդարտ ստացման՝ այս այլընտրաքային մեթոդը մինչև վերջին քայլը խուսափում է կոտորակների ու քառակուսային ֆունկցիաների կիրառումից, և այդպիսով երրորդ քայլից հետո ընդհանուր հայտարարի բերման համար վերադասավորում չի պահանջում[12]։
Երրորդ մեթոդ
խմբագրելԱռաջին՝ ստանդարտ մեթոդի նման, բաժանել հավասարման երկու կողմը ֊ով՝ քառակուսային փոփոխականի գործակիցը դարձնելու համար․
Արտագրել հավասարումն ավելի սեղմ ու հեշտ ընթեռնելի ձևով․
որտեղ և ։ Լրացնել քառակուսին՝ առաջին երկու անդամին գումարելով, իսկ երրորդից՝ հանելով․
Խմբավորել ձախ կողմը՝ քառակուսիների տարբերություն ստանալու համար․
Ֆակտորիզացնել այն․
ինչից հետևում է
կամ
Հավասարումներից յուրաքանչյուրը կարող ենք լուծել ֊ի համար՝ ստանալով․
կամ
Ներկայացնելով ֊ի ու ֊ի նախնական արժեքները՝ կստանաք օրիգինալ քառակուսային բանաձևը։
Փոխարինմամբ
խմբագրելԼուծման մեկ այլ տեխնիկա է փոխարինումը[14]։ Այս տեխնիկայով մենք փոխարինում ենք քառակուսային հավասարման մեջ և ստանում հավասարումը։ Բացելով փակագծերն ու անհայտի աստիճաններն իրար հետ հավաքելով ստանում ենք․
Քանի որ ո՛չ ֊ի, ո՛չ ֊ի համար որևէ սահմանափակում նկարագրված չէր, մենք կարող ենք ֊ն այնպես ընտրել, որ միջին անդամն անհետանա։ Այսինքն՝ կամ : Հավասարման երկու կողմից ազատ անդամը հանելով, ապա՝ ֊ով բաժանելով (նկատեք, որ, ըստ սահմանման ), ստանում ենք․
Փոխարինելով ֊ի արժեքը․
Այդպիսով․
Այժմ կարող ենք կրկին փոխարինել ֊ի արժեքը՝ ֊ով արտահայտված, օգտագործելով հավասարումը։ Արդյունքում կստանանք սովորական քառակուսային բանաձևը․
Հանրահաշվական նույնություններով
խմբագրելՀետևյալ մեթոդը պատմական տարբեր շրջաններում բազմաթիվ մաթեմատիկոսներ են օգտագործել․[15]
դիցուք, ֊ը և ֊ը ստանդարտ քառակուսային հավասարման արմատներն են։ Բանաձևի ստացումը սկսվում է հետևյալ նույնությամբ․
Յուրաքանչյուր կողմից քառակուսի արմատ հանենք․
Քանի որ հավասարման քառակուսային անդամի գործակիցը՝ ֊ն, ըստ սահմանման , կարող ենք ստանդարտ հավասարումը բաժանել -ի վրա՝ նույն արմատներն ունեցող քառակուսային բազմանդամ ստանալու համար․
Այստեղից կարող ենք տեսնել, որ քառակուսային հավասարման արմատների գումարը պետք է հավասար լինի , իսկ արտադրյալը՝ ։ Այդպիսով, նույնությունը կարող ենք գրել հետևյալ տեսքով․
Այժմ,
Քանի որ , եթե օգտագործենք , կստանանք․
Իսկ եթե վերցնենք , կարող ենք հաշվել նաև հետևյալ բանաձևը․ ։
Արդյունքները ստանդարտ նշանով միացորելով, ստանում ենք քառակուսային հավասարման լուծումները գտնելու հետևյալ բանաձևը․
Պատմությունը
խմբագրելՔառակուսային հավասարումներ լուծելու ամենավաղ հայտնաբերված եղանակը երկրաչափականն է։ Բաբելոնյան սեպագիր հուշատախտակներում խնդիրներ կան, որոնք կարելի է լուծել քառակուսային հավասարում ներկայացնելով[16]։ Եգիպտական Բեռլինի Պապիրուսը, որը ժամանակագրվում է Միջին Թագավորության (մ․թ․ա․ 2050 ֊ մ․թ․ա․ 1650 թվականներ) ժամանակաշրջան, երկու անդամով քառակուսային հավասարումների լուծման եղանակներ է պարունաում[17]։
Հույն մաթեմատիկոս Էվկլիդեսը (մ․թ․ա․ 300) իր Սկզբունքներ երկի երկրորդ գրքում քառակուսային հավասարումներ լուծեու երկրաչափական եղանակներ է նկարագրել[18]։ Քառակուսային հավասարման կանոնները հանդիպում են նաև չինական Ինը Գլուխ Մաթեմատիկական Արվեստի մասին աշխատությունում (մ․թ․ա․ 200)[19][20]։ Իր Թվաբանություն աշխատությունում հույն մաթեմատիկոս Դիոֆանտը (մոտ․ 250 թվական) քառակուսային հավասարումներ է լուծում հանրահաշվականին ավելի մոտ եղանակով, քան Էվկլիդեսի նկարագրած երկրաչափական հանրահաշիվն էր[18]։ Դիոֆանտի եղանակը հավասարման միայն մի լուծումն է գտնում, նույնիսկ այն դեպքում, երբ երկու արմատներն էլ դրական են[21]։
Հնդիկ մաթեատիկոս Բրահմագուպտան (597–668 թվականներ) հստակ նկարագրել է քառակուսային բանաձևն իր Բրահմայի ուսմունքի կատարելագործում գրքում, որը հրատարակվել է 628 թվականին[22], սակայն նկարագրել է այն բառերով՝ առանց նշաններ օգտագործելու[23]։ Բրահմագուպտայի՝ քառակուսային հավասարում լուծելու առաջարկած եղանակը հետևյալն էր․ «բացարձակ թվի (քառակուսու գործակցի) քառապատիկի արտադրյալին գումարե՛ք միջին անդամի (գործակցի) քառակուսին; նույնի քառակուսի արմատը, հանած միջին անդամը (միջին անդամի գործակիցը), բաժանած քառակուսու (գործակցի) կրկնապատիկով, (և կստանաք) արժեքը»[24]։ Ինչը համարժեք է բանաձևին։
9֊րդ դարի պարսիկ մաթեմատիկոս Մուհամեդ իբն Մուսա Խորեզմին հանրահաշվորեն քառակուսային հավարումներ է լուծել[25]։ Բոլոր հնարավոր դեպքերը հաշվի առնող առաջին բանաձևը հայտնաբերել է Սիմոն Սթևինը 1594 թվականին[26]։ 1637 թվականին Ռենե Դեկարտը հրատարակել է Երկրաչափությունը, որտեղ ներկայացրել է մեր՝ այսօր օգտագործվող քառակուսային բանաձևի կիրառման հատուկ դեպքերը[27]։
Կիրառումներ
խմբագրելԵրկրաչափական կիրառում
խմբագրելՊարաբոլը ցանկացած կոր է, որի - կոորդինատները սահմանվում են երկրորդ աստիճանի բազմանդամով․ , որտեղ -ն ներկայացնում է երկրորդ աստիճանի բազմանդամը, իսկ և գործակից հաստատուններ են, որոնց ինդեքսները համընկնում են իրենց համապատասխան անհայտի աստիճանին։ Երկրաչափական մեկնաբանությամբ, քառակուսային բանաձևը սահմանում է այն կետերը, որտեղ պարաբոլը կհատի ֊երի առանցքը։ Ավելին․ եթե քառակուսային հավասարումը դիտարկվի երկու անդամով․
Համաչափության առանցքը կհամընկնի ուղղի հետ։ Մյուս անդամը՝ , ներկայացնում է արմատների հեռավորությունը համաչափության առանցքից։ Արմատներից մեկը «դրական»՝ դեպի աջ, հեռավորություն ունի, մյուսը՝ «բացասական», դեպի ձախ։
Եթե արմատների հեռավորությունը համաչափության առանցքից հասնում է զրոյի, համաչափության առանցքի արժեքը հավասար կլինի արմատի արժեքին՝ այն արժեքին, որում ֆունկցիայի արժեքը հավասար է զրոյի։ Այսինքն՝ քառակուսային հավասարումը միայն մի լուծում ունի։ Հանրահաշվորեն սա նշանակում է, որ , այսինքն․ ։ Նկատեք, որ հավասարման ձախ հատվածը պարզապես դիսկրիմինանտն է։
Դիսկրիմինանտի արժեքը ցույց է տալիս, թե պարաբոլը քանի զրո կունենա։ Երեք հնարավոր դեպք կա․ դիսկրիմինանտը կարող է լինել դրական, ինչի դեպքում հեռավորությունը նույնպես դրական կլինի, և պարաբոլը երկու զրո կունենա, հավասարումն էլ, համապատասխանաբար՝ երկու իրական լուծում։ Սակայն, երբ դիսկրիմինանտը բացասական է, հեռավորությունը կեղծ է՝ կոմպլեք արմատ թվի որևէ իրական բազմատիկ, ինչը նշանակում է, որ պարաբոլի զրոները կոմպլեքս թվեր են։
Քառակուսային հավասարման կոմպլեքս արմատները կոմպլեքս զույգեր են, որոնց իրական մասի արժեքը հավասար է համաչափության առանցքի արժեքին։ Նման պարաբոլը որևէ իրական արժեքի համար -երի առանցքը չի հատի։
Տարածական անալիզ
խմբագրելԵթե և հաստատուններն անմիավոր չեն, -ի միավորը պետք է հավասար լինի մեծության միավորին, քանի որ հավասարման և անդամները պետք է նույն միավորն ունենան։ Ավելին՝ նույն տրամաբանությամբ հաստատունի միավորը պետք է համընկնի մեծության միավորին, ինչը կարող ենք հաստատել առանց հավասարումը լուծելու։ Այս փաստը հնարավորություն է տալիս քառակուսային հավասարումը լուծելուց առաջ ստուգել, արդյո՞ք ֆիզիկական մեծություններ արտահայտող հավասարումը ճիշտ է սահմանված, թե՞՝ ոչ։
Տեսեք նաև
խմբագրելԾանոթագրություններ
խմբագրել- ↑ «Քառակուսային Ֆակտորիզացիա․ Ամբողջական ուղեցույց». Մեթ Վոլտ (անգլերեն). 2016, մարտի 13. Վերցված է 2019, նոյեմբերի 10-ին.
- ↑ Ստեռլինգ, Մերի Ջեյն (2010), Հանրահաշիվ I Հիմարիկների համար, Wiley Publishing, էջ 219, ISBN 978-0-470-55964-2
- ↑ «Հասկանանք Քառակուսային բանաձևը». Khan Academy (անգլերեն). Վերցված է 2019, նոյեմբերի 10-ին.
- ↑ «Պարաբոլի Համաչափության Առանցքները․ Ինչպես գտնել առանցքները գրաֆիկից։ Համաչափության առանցքները գտնելու համար․․․». www.mathwarehouse.com. Վերցված է 2019, նոյեմբերի 10-ին.
- ↑ «Դիսկրիմինանտի ամփոփում». Khan Academy (անգլերեն). Վերցված է 2019, նոյեմբերի 10-ին.
- ↑ Կահան, Ուիլիամ (2004, նոյեմբերի 20), On the Cost of Floating-Point Computation Without Extra-Precise Arithmetic (PDF), Վերցված է 2012, դեկտեմբերի 25-ին
- ↑ «Քառակուսային բանաձև», Ապացույցների Վիքի, Վերցված է 2016, հոկտեմբերի 08-ին
- ↑ Ռիչ, Բարնեթ; Շմիթ, Ֆիլիպ (2004), Տարրական Հանրահաշվի Թեորիայի ու Խնդիրների Շոմի Ուրվագիծը, The McGraw – Hill Companies, ISBN 0-07-141083-X, Գլուխ 13 §4.4, էջ 291
- ↑ Լի, Շուհույ (2007). Միջին դպրոցի հանրահաշվի ուսուցիչների հանրահաշվական հավասարումների լուծման դասավանդման գիտելիքի հետազոտություն. ProQuest. էջ 56.
- ↑ Ռոքսվոլդ, Գերի (2002). Համալսարանական հանրահաշիվ և եռանկյունաչափություն և նախնական անալիզ. Addison Wesley. էջ 178.
- ↑ Բեքենբախ, Էդվին (1986). Ժամանակակից համալսարանական հանրահաշիվ և եռանկյունաչափություն. Wadsworth Pub. Co. էջ 81.
- ↑ 12,0 12,1 Հոեն, Լերրի (1975). «Քառակուսային բանաձևի ստացման առավել էլեգանտ մեթոդ». Մաթեմատիկայի Ուսուցիչը. 68 (5): 442 ֊ 443.
- ↑ Սմիթ, Դեյվիդ Ի․ (1958). Մաթեմատիկայի Պատմություն, Հատոր II. Dover Publications. էջ 446. ISBN 0486204308.
- ↑ Ջոզեֆ Ջ․ Րոթման։ (2010)։ Ժամանակակից Առաջադեմ Հանրահաշիվ։ (Հատոր 114)։ Ամերկյան Մաթեմատիկոսների Հասարակություն։ Բաժին 1.1
- ↑ Դեբնաթ, Լոքենաթ (2009). «Լեոնարդ Էյլերի ժառանգությունը – երեքդարյա հարգանքի տուրք». Գիտությունների և Տեխնոլոգիայի Մաթեմատիկական կրթության Միջազգային Ամսագիր. 40 (3): 353–388. doi:10.1080/00207390802642237. S2CID 123048345.
- ↑ Իրվինգ, Ռոն (2013). Քառակուսային բանաձևից այն կողմ. MAA. էջ 34. ISBN 978-0-88385-783-0.
- ↑ Քեմբրիջի Հնագույն Պատմություն Մաս 2․ Միջին Արևելքի Հին Պատմություն. Cambridge University Press. 1971. էջ 530. ISBN 978-0-521-07791-0.
- ↑ 18,0 18,1 Իրվինգ, Ռոն (2013). Քառակուսային բանաձևից այն կողմ. MAA. էջ 39. ISBN 978-0-88385-783-0.
- ↑ Այտկեն, Ուեյն. «Չինական Դասականներ․ Ինը Գլուխները» (PDF). Մաթեմարիկայի Ֆակուլտետ, Կալիֆոռնիայի Պետական Համալսարան. Վերցված է 2013, ապրիլի 28-ին.
- ↑ Սմիթ, Դեյվիդ Յուջին (1958). Մաթեմատիկայի Պատմություն. Courier Dover Publications. էջ 380. ISBN 978-0-486-20430-7.
- ↑ Սմիթ, Դեյվիդ Յուջին (1958). Մաթեմատիկայի պատմություն. Courier Dover Publications. էջ 134. ISBN 0-486-20429-4.
- ↑ Բրեդլի, Մայքլ Մաթեմատիկայի Ծնունդը․ Հնագույն ժամանակներից 1300 թվական, էջ 86 (Infobase Publishing 2006)
- ↑ Մաքքենզի, Դեյնա Տիեզերքը Զրո Բառով․ Մաթեմատիկայի պատմությունը՝ Հավասարումների միջոցով, էջ 61 (Princeton University Press, 2012)
- ↑ Սթիլվել, Ջոն (2004). Մաթեմատիկան ու դրա Պատմությունը (2-րդ հրատ․). Springer. էջ 87. ISBN 0-387-95336-1.
- ↑ Իրվինգ, Ռոն (2013). Քառակուսային բանաձևից այն կողմ. MAA. էջ 42. ISBN 978-0-88385-783-0.
- ↑ Ստրուիկ, Դ․ Ջ․; Սթևին, Սիմոն (1958), Սիմոն Սթևինի հիմնական գործերը, Մաթեմատիկա (PDF), vol. II–B, C. V. Swets & Zeitlinger, էջ 470
- ↑ Ռենե Դեկարտ. Երկրաչափություն (անգլերեն).











