Ռադիան
Ռադիան (նշանակումը՝ ռադ, rad; լատ.՝ radius - աղեղ, շառավիղ բառից), Միավորների միջազգային համակարգում և մաթեմատիկայի բազմաթիվ ոլորտներում անկյունների չափման միավոր։
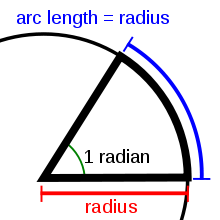
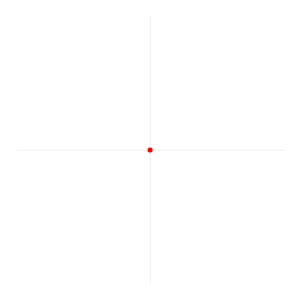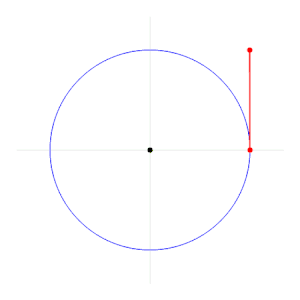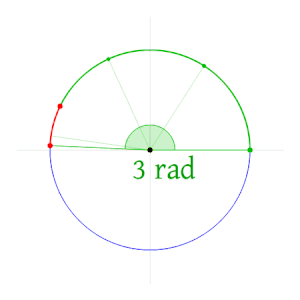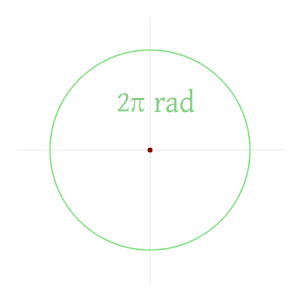
Այն կենտրոնական անկյունը, որի հենման աղեղի երկարությունը հավասար է շրջանագծի շառավղին, կոչվում է մեկ ռադիան մեծությամբ անկյուն[1]։ Արտահայտված աստիճաններով մեկ ռադիանը հավասար է մոտ 57.3 աստիճանի (համաձայն A072097 ): Միավորը նախկինում համարվում էր SI լրացուցիչ միավոր, սակայն միավորների այս կատեգորիան վերացվել է 1995 թվականին, և ռադիանը այժմ համարվում է SI ածանցյալ միավոր[2]։
Տարածաչափական, ոչ հարթ անկյունների չափման միավորը ՍԻ համակարգում կոչվում է ստեռադիան։
Ռադիանը հիմնականում նշանակվում է rad նշանով (Յունիկոդում՝ U+33AD ㎭)[3]: Այլընտրանքային նշանն է՝ c, լատինական c տառի վերտողային գրառումը (անգլերեն «circular measure» «շրջանային չափ»), r տառը կամ վերտեղային R[4], բայց այդ գրառման տարբերակները հազվադեպ են օգտագործվում, քանի որ այն հեշտությամբ կարելի է շփոթել աստիճանի նշանի (°) կամ շառավղի (r) նշանակումների հետ։ Այսպիսով, օրինակ, 1,2 ռադիանի արժեքը կարող է գրվել որպես 1,2 ռադ, 1,2 rad, 1,2 r, 1,2 rad, 1,2 c կամ 1,2 R:

Պատմություն
խմբագրելԱնկյան աստիճանի փոխարեն ռադիանով չափման գաղափարը վերագրվում է Ռոջեր Քոթսին[5][6]։ 1714 թվականին նա առանց ռադիան անվանում տալու, նկարագրում է նման չափումների գաղափարը և նշում, որ դա բնական միավոր կլիներ։ Անկյունները աղեղի երկարությամբ չափելու գաղափարը մինչ այդ օգտագործվում էր այլ մաթեմատիկոսների կողմից։ Օրինակ, ալ-Կաշին (մոտ 1400 թվականին), օգտագործել էր այսպես կոչված տրամաչափի մասեր միավորը, որտեղ մեկ տրամագծի մասը հավասար էր 160 ռադիանի և նաև կիրառվում էր, տրամաչափի մասի 60–րդ մասեր[7]։
Ռադիան եզրույթը առաջին անգամ տպված վիճակում հանդիպում է 1873 թվականի հունիսի 5-ին, Բելֆաստի Քվինս համալսարանի քննական հարցաշարում, որի հեղինակն էր ֆիզիկոս և ճարտարագետ Ջեյմս Թոմսոնը (Լորդ Քելվինի եղբայրը)։ Նա օգտագործում էր այդ տերմինը դեռ 1871 թվականին, իսկ 1869 թվականին Թոմաս Մուիրը (Սուրբ Էնդրյուսի համալսարան) տատանվում էր «ռադ», «ռադիալ» և «ռադիան» տարբերակների միջև։ 1874 թվականին, Ջեյմս Թոմսոնի հետ խորհրդակցելուց հետո, Մուիրը անցավ ռադիան տարբերակին[8][9][10]։
Փոխարկում
խմբագրել| Պտույտ | Ռադիան | Աստիճան | Գռադիան |
|---|---|---|---|
| 0 | 0 | 0° | 0g |
| 124 | π12 | 15° | 16 23g |
| 112 | π6 | 30° | 33 13g |
| 110 | π5 | 36° | 40g |
| 18 | π4 | 45° | 50g |
| 12π | 1 | ~ 57.3° | ~ 63.7g |
| 16 | π3 | 60° | 66 23g |
| 15 | 2π5 | 72° | 80g |
| 14 | π2 | 90° | 100g |
| 13 | 2π3 | 120° | 133 13g |
| 25 | 4π5 | 144° | 160g |
| 12 | π | 180° | 200g |
| 34 | 3π2 | 270° | 300g |
| 1 | 2π | 360° | 400g |
Ռադիանների և անկյունների միջև փոխարկում
խմբագրելԻնչպես նշվել է մեկ ռադիանը հավասար է 180/π աստիճանի։ Այդպիսով, ռադիանը աստիճանով փոխարկելու համար, այն պետք է բազմապատկել 180/π.
Օրինակ՝
Հակառակը՝ աստիճանը ռադիանով փախարկելու համար այն պետք է բազմապատկել π/180։
Օրինակ՝
Ռադիանները կարելի է փոխարկել պտույտներով (ամբողջական 360° պտույտով) ռադիանով արժեքը բաժանելով 2π–ով։
Ռադիանի աստիճանի փոխարկման դուրսբերում
խմբագրելՇրջանագծի պարագիծը հավասար է , որտեղ շրջանագծի շառավիղն է։
Այսպիսով ճիշտ է հետևյալ հավասարումը՝
[Քանի որ անհրաժեշտ է պտույտ, ամբողջ շրջան նկարելու համար]
Ըստ ռադիանի սահմանման, ամբողջ պտույտը հավասար է
Համադրելով վերևի 2 հարաբերությունները, կստանանք՝
Ռադիանից գռադիանի փոխարկում
խմբագրելռադիանը հավասար է մեկ պտույտի, որը ըստ սահմանման հավասար է 400 Գռադիանի (400g)։ Այսպիսով, ռադիանոց գռադիան փոխակերպելու համար պետք է բազմատկել –ով, իսկ գռադիաններից ռադիանների փոխարկելու համար բազմապատկել ։
Օրինակ՝
Ռադիաններով չափման առավելությունները
խմբագրելՄաթեմատիկական անալիզում և կիրառական երկրաչափությունից բացի, մաթեմատիկայի գրեթե բոլոր ճյուղերում անկյունները չափվում են ռադիաններով։ Դա պայմանավորված է նրանով, որ ռադիանները մաթեմատիկորեն «բնական» են, ինչը թույլ է տալիս ավելի պարզ և գեղեցիկ տեսքով գրառել մի շարք կարևոր արտահայտություններ։
Օրինակ, Եռանկյունաչափական ֆունկցիաները ավելի պարզ և գեղեցիկ տեսք են ստանում, երբ արգումենտները արտահայտված են ռադիաններով։ Օրինակ ֆունկցիայի սահմանը ստանում է հետևյալ տեսքը՝
ինչը հանդիսանում է շատ այլ արտահայտությունների հիմքը՝
Այս և այլ հատկությունների հաշվին, եռանկյունաչափական ֆունկցիաները հայտնվում են լուծումներում, որոնք առաջին հայացքից կապ չունեն ֆունկցիաների երկրաչափական իմաստի հետ (օրինակ դիֆֆերենցիալ հավասարուման մեջ՝ կամ ինտեգրալի վերլուծության՝ )։ Բոլոր նման դեպքերում ֆունկցիաների արգումենտները առավել բնական տեսք են ստանում, երբ գրված են ռադիանով չափված անկյան ձևով։
Եռանկյունաչափական ֆունկցիաները նաև պարզ ու գեղեցիկ տեսք են ստանում հաջորդականությունների մեջ։ Օրինակ այս sin x–ի Թեյլորի շարքում՝
Եթե x արտահայտված լիներ աստիճաններով, ապա շարքը կունենա դժվար ընթեռնելի տեսք և կներառի π/180–ի աստիճաններով բազմապատկիչներ՝ եթե x աստիճանով արժեքն է, ապա ռադիաններով արժեք կլինի y = π x / 180, և այդպիսով կստանանք
Սինուսի, կոսինուսի և ցուցչային ֆունկցիայի միջև մաթեմատիկայում կարևոր հարաբերությունը (օրինակ՝ Էյլերի բանաձևը) կրկին ֆունկցիաների արգումենտները ռադիաններով արտահայտված լինելու դեպքում ստանում են ավելի գեղեցիկ տեսք, և դժվարընթեռնելի են այլապես։
Ծանոթագրություններ և նշումներ
խմբագրել- ↑ «Ռադիան, դրական և բացասական պտույտներ. Զաբելա Աբելյան - Պաշարների շտեմարան». lib.armedu.am. Արխիվացված է օրիգինալից 2017 թ․ նոյեմբերի 12-ին. Վերցված է 2019 թ․ մարտի 2-ին.
- ↑ «Resolution 8 of the CGPM at its 20th Meeting (1995)». Bureau International des Poids et Mesures. Վերցված է 2014 թ․ սեպտեմբերի 23-ին.
- ↑ Յունիկոդի նշանն է U+33AD ㎭ հին այլագրումների հետ համատեղելիության համար
- ↑ Hall, Arthur Graham; Frink, Fred Goodrich (January 1909). «Chapter VII. The General Angle [55] Signs and Limitations in Value. Exercise XV.». Written at Ann Arbor, Michigan, USA. Trigonometry. Vol. Part I: Plane Trigonometry. New York, USA: Henry Holt and Company / Norwood Press / J. S. Cushing Co. - Berwick & Smith Co., Norwood, Massachusetts, USA. էջ 73. Վերցված է 2017 թ․ օգոստոսի 12-ին.
{{cite book}}: CS1 սպաս․ url-status (link) - ↑ O'Connor, J. J.; Robertson, E. F. (February 2005). «Biography of Roger Cotes». The MacTutor History of Mathematics. Արխիվացված է օրիգինալից 2012 թ․ սեպտեմբերի 24-ին. Վերցված է 2019 թ․ մարտի 2-ին.
- ↑ Ռոջեր Քոթսը մահացավ 1716–ին։ 1722 թվականին, իր մորաքրոջ տղեն Ռոբերտ Սմիթը հավաքել և հարապարակել էր Քոթսի մաթեմատիկական աշխատանքները գրքի տեսքով, որն անվանել էր Harmonia mensurarum։ Խմբագրողի կողմից մեկնաբանության բաժնում, նա առաջին անգամ տալիս է ռադիանը արժեքը անկյուններով։Տես՝ Roger Cotes with Robert Smith, ed., Harmonia mensurarum … (Cambridge, England: 1722), chapter: Editoris notæ ad Harmoniam mensurarum, top of page 95 էջ 95–ում, այն հատվածից հետո, որբ նա նշում է, որ 180° կհամապատասխանի π (3.14159…) երկարությանը (այսինքն ռադիանի), Սմիթը գրում է․ "Unde Modulus Canonis Trigonometrici prodibit 57.2957795130 &c. " (Whence the unit of trigonometric measure, 57.2957795130… [degrees per radian], will appear.)
- ↑ Luckey, Paul (1953) [Translation of 1424 book]. Siggel, A. (ed.). Der Lehrbrief über den kreisumfang von Gamshid b. Mas'ud al-Kasi [Treatise on the Circumference of al-Kashi]. Berlin: Akademie Verlag. էջ 40.
- ↑ Cajori, Florian (1929). History of Mathematical Notations. Vol. 2. էջեր 147–148. ISBN 0-486-67766-4.
- ↑ Muir, Thos. (1910). «The Term "Radian" in Trigonometry». Nature. 83 (2110): 156. Bibcode:1910Natur..83..156M. doi:10.1038/083156a0.Thomson, James (1910). «The Term "Radian" in Trigonometry». Nature. 83 (2112): 217. Bibcode:1910Natur..83..217T. doi:10.1038/083217c0.Muir, Thos. (1910). «The Term "Radian" in Trigonometry». Nature. 83 (2120): 459–460. Bibcode:1910Natur..83..459M. doi:10.1038/083459d0.
- ↑ Miller, Jeff (2009 թ․ նոյեմբերի 23). «Earliest Known Uses of Some of the Words of Mathematics». Վերցված է 2011 թ․ սեպտեմբերի 30-ին.
