Մակընթացային փական
Մակընթացային փականը առաջանում է երկու իրար շուրջ պտտվող աստղագիտական մարմինների միջև, երբ մարմիններից մեկը հասնում է մի վիճակի, երբ ամբողջական ուղեծրային պտույտի ընթացքում նրա կատարած իր առանցքի շուրջ պտույտների պարբերությունում որևէ փոփոխություն չի տեղի ունենում։ Այն դեպքում, երբ մակընթացային փականված մարմինը սինքրոն պտույտ ունի, այն պտտվում է իր առանցքի շուրջը նույն ժամանակում, որքան իր ուղեծրի պտույտի պարբերությունն է։ Օրինակ, Լուսնի միշտ միևնույն կողմն է շրջված դեպի Երկիր, թեև լիբրացիայի հետևանքով Լուսնի ուղեծիրը կատարյալ շրջանաձև չէ։ Սովորաբար, միայն բնական արբանյակն է մակընթացայնորեն փականված ավելի մեծ մարմնի հետ[1]։ Այնուամենայնիվ, եթե երկու մարմինների միջև և՛ զանգվածի տարբերությունը, և՛ նրանց միջև հեռավորությունը համեմատաբար փոքր են, յուրաքանչյուրը կարող է մակընթացային կերպով փականվել մյուսի հետ. սա Պլուտոնի-Քարոնի, կամ ինչպես նաև Էրիսի և Դիսնոմիայի դեպքում է։ Մակընթացային փականը նաև անվանում են «գրավիտացիոն փական»[2], կամ «գրավված պտույտ», կամ «պտտվող ուղեծրի փականում»։
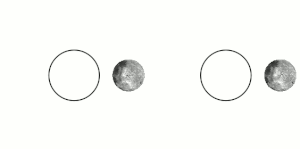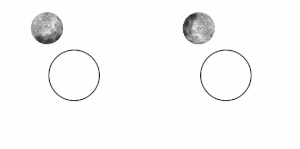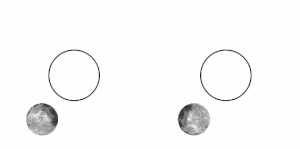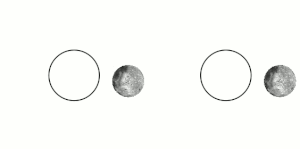
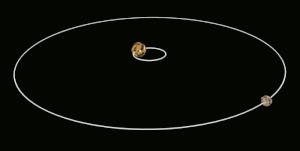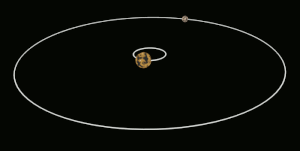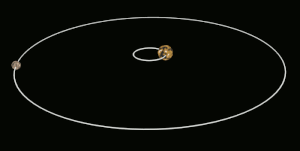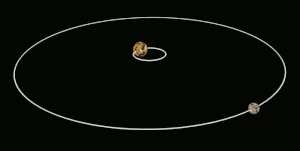
Այս էֆեկտն առաջանում է երկու մարմինների միջև, երբ նրանց գրավիտացիոն փոխազդեցությունը դանդաղեցնում է մարմնի պտույտը իր առանցքի շուրջ, մինչև այն ընկնում է մակընթացային փականի մեջ։ Միլիոնավոր տարիների ընթացքում էներգիայի փոխանակման և ջերմության ցրման երևությների փոխազդեցության ուժերի ազդեցությամբ փոխվում են մարմինների ուղեծրերը և պտույտի պարբերությունները։ Երբ մարմիններից մեկը հասնում է մի վիճակի, որտեղ այլևս չկա որևէ փոփոխություն նրա պտույտի պարբերության մեջ մեկ ամբողջական ուղեծրի ընթացքում, ասում են, որ այն մակընթացայնորեն փականված է[3]։ Մարմինները հակված են մնալու այս վիճակում, քանի որ այս վիճակից դուրս գալը ենթադրում է էներգիայի գործադրում համակարգին։ Օբյեկտի ուղեծիրը կարող է ժամանակի ընթացքում փոփոխվել, այս դեպքում մակընթացային փականը կարող է խախտվել, օրինակ, եթե հսկա մոլորակի ազդեցությունը բերում է մարմնի ուղեծրի փոփոխությունների։
Մակընթացային փականի ոչ բոլոր դեպքերն են ենթադրում սինքրոն պտույտ[4]։ Մերկուրիի դեպքում, օրինակ, մակընթացային փականի պարագայում մոլորակը Արեգակի շուրջ յուրաքանչյուր երկու պտույտի ընթացքում կատարում է երեք պտույտ իր առանցքի շուրջ՝ 3:2 պարբերությամբ ռեզոնանս։ Հատուկ դեպքերում, երբ ուղեծիրը գրեթե շրջանաձև է, և մարմնի պտույտի առանցքը զգալիորեն թեքված չէ, օրինակ՝ Լուսինը, մակընթացային փականը հանգեցնում է նրան, որ պտտվող մարմնի միայն միևնույն կիսագունդն է ուղղված դեպի մյուս մարմինը[3][4][5]։ Այնուամենայնիվ, այս դեպքում մարմնի ճիշտ նույն մասը միշտ չէ, որ ուղղված է դեպի մյուս մարմինը։ Փականված մարմնի ուղեծրային արագության և նրա պտտման առանցքի թեքության տատանումների պատճառով կարող է լինել որոշակի պարբերական տեղաշարժ։
Տես նաև խմբագրել
Ծանոթագրություններ խմբագրել
- ↑ «When Will Earth Lock to the Moon?». Universe Today. 2016 թ․ ապրիլի 12.
- ↑ Clouse, Christopher; և այլք: (May 2022). «Spin-orbit gravitational locking-an effective potential approach». European Journal of Physics. 43 (3): 13. arXiv:2203.09297. Bibcode:2022EJPh...43c5602C. doi:10.1088/1361-6404/ac5638. S2CID 246962304. 035602.
{{cite journal}}: CS1 սպաս․ postscript (link) - ↑ 3,0 3,1 Barnes, Rory, ed. (2010). Formation and Evolution of Exoplanets. John Wiley & Sons. էջ 248. ISBN 978-3527408962.
- ↑ 4,0 4,1 Heller, R.; Leconte, J.; Barnes, R. (April 2011). «Tidal obliquity evolution of potentially habitable planets». Astronomy & Astrophysics. 528: 16. arXiv:1101.2156. Bibcode:2011A&A...528A..27H. doi:10.1051/0004-6361/201015809. S2CID 118784209. A27.
- ↑ Mahoney, T. J. (2013). Mercury. Springer Science & Business Media. ISBN 978-1461479512.