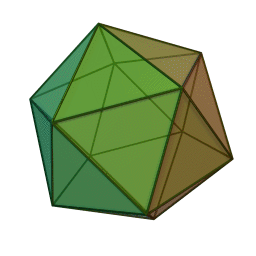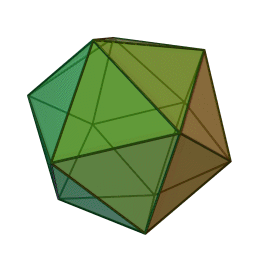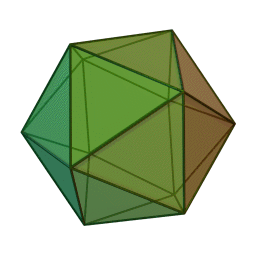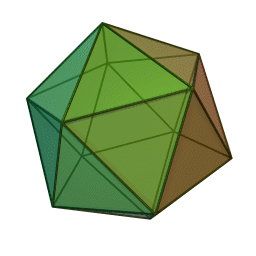
Կանոնավոր քսանանիստ
| Կանոնավոր քսանանիստ | |
|---|---|
|
|
| Տիպ | Կանոնավոր բազմանիստ |
| Նիստերի տեսքը | Հավասարակողմ եռանկյուն |
| Նիստեր | 20 |
| Կողեր | 30 |
| Գագաթներ | 12 |
| Մի գագաթից դուրս եկող նիստեր | 5 |
| Մակերևույթի մակերես | |
| Ծավալ | |
| Ներգծյալ գնդի շառավիղ | |
| Արտագծյալ գնդի շառավիղ | [1] |
| Սիմետրիայի խումբ | Икосаэдрическая (Ih) |
Կանոնավոր քսանանիստ կամ կանոնավոր իկոսաէդր (հին հունարեն՝ εἴκοσι «քսան», ἕδρον «նիստ», «հիմք»), կանոնավոր ուռուցիկ բազմանիստ, քսանանիստ[2], Պլատոնական մարմիններից մեկը։ 20 նիստերից յուրաքանչյուրը հավասարակողմ եռանկյուն է։ Կողերի քանակը 30 է, գագաթների թիվը՝ 12: Քսանանիստն ունի 59 աստղային տեսք։
Պատմություն
խմբագրելԷվկլիդեսը իր «Սկզբունքներ» XIII գրքի 16-րդ բաժնում, ուսումնասիրում է քսանանիստի կառուցվածքը, նախ ստանալով երկու կանոնավոր հնգանկյուն՝ ընկած երկու զուգահեռ հարթություններում, իր տաս գագաթներով, այնուհետև` միմյանց հակառակ երկու մնացած գագաթները[3][4]։ Պապուս Ալեքսանդրացին իր «Մաթեմատիկական ժողովածուում» զբաղվում է քսանանիստի կառուցմամբ՝ ապացուցելով, որ նրա տասներկու գագաթները գտնվում են չորս զուգահեռ հարթություններում՝ դրանցում կազմելով չորս կանոնավոր եռանկյունի[4][5]:
Հիմնական բանաձևեր
խմբագրելa կողով քսանանիստի S մակերևույթի մակերեսը, V ծավալը, ինչպես նաև ներգծված և արտագծված գնդերի շառավիղները հաշվարկվում են հետևյալ բանաձևերով.
Մակերես՝
Ծավալ՝
Ներգծված գնդի շառավիղ[1]՝
Արտագծված գնդի շառավիղ[1]՝
Հատկություններ
խմբագրել- Քսանանիստի ցանկացած երկու հարևան նիստերի միջև երկնիստ անկյունը հավասար է arccos(-√5 / 3) = 138.189685°:
- Քսանանիստի բոլոր տասներկու գագաթներից երեքական ընկած են չորս զուգահեռ հարթություններում՝ յուրաքանչյուրից կազմելով կանոնավոր եռանկյուն։
- Քսանանիստի տասը գագաթները գտնվում են երկու զուգահեռ հարթություններում, դրանցում կազմելով երկու կանոնավոր հնգանկյուն, իսկ մյուս երկուսը՝ միմյանց հակադիր են և ընկած են ներգծված գնդի տրամագծի երկու ծայրերում, ուղղահայաց այս հարթություններին։
- Քսանանիստը կարող է ներգծվել խորանարդի մեջ, այս դեպքում, քսանանիստի վեց փոխուղղահայաց կողերը կգտնվեն, համապատասխանաբար, խորանարդի վեց նիստերի վրա, մնացած 24 կողերը գտնվում են խորանարդի ներսում, քսանանիստի բոլոր տասներկու գագաթները ընկած կլինեն խորանարդի վեց նիստերի վրա։
- Քսանանիստին կարելի է ներգծել տետրաեդր, այնպես, որ քառանիստի(տետրաեդրի), չորս գագաթները կհամնկնեն քսանանիստի չորս գագաթների հետ։
- Քսանանիստը կարող է ներգծվել դոդեկադրի մեջ, այս դեպքում քսանանիստի գագաթները կհամընկնեն դոդեկաեդրի նիստերի կենտրոններին։
- Քսանանիստի մեջ կարող է ներգծվել դոդեկաեդր՝ դոդեկաեդրի գագաթների եւ քսանանիստի նիստերի կենտրոնների համընկնումով։
- Հատած քսանանիստ կարելի է ստանալ 12 գագաթներ կտրելով կանոնավոր հնգանկյունների տեսքով նիստերի ձևավորմամբ։ Այս դեպքում նոր բազմանիստի գագաթների թիվը ավելանում է 5 անգամ (12 × 5 = 60), 20 եռանկյուն նիստերը վերածվում են սովորական վեցանկյունների (նիստերի ընդհանուր թիվը դառնում է 20 + 12 = 32), իսկ կողերի թիվը մեծանում է մինչեւ 30 + 12 × 5 = 90:
- Քսանանիստի մոդելը կարելի է հավաքել՝ օգտագործելով 20 հավասարակողմ եռանկյուն։
- Անհնար է քսանանիստ պատրաստել կանոնավոր տետրաեդրից, քանի որ քսանանիստին ներգծված գնդի շառավիղը, և հետևաբար տետրաեդրի կողմնային կողերի երկարությունը (գագաթից մինչև նման հավաքածուի կենտրոն) փոքր է քսանանիստի կողից։
Հատած քսանանիստ
խմբագրելՀատած քսանանիստ, բազմանիստ՝ բաղկացած 12 կանոնավոր հինգանկյունուց և 20 կանոնավոր վեցանկյունուց։ Այն ունի իկոսաեդանման համաչափություն։ Իրականում, դասական ֆուտբոլի գնդակը ոչ թե գնդակ է, այլ հատած քսանանիստ՝ ուռուցիկ (գնդաձև) կողերով:։
Աշխարհում
խմբագրել- Քսանանիստը կանոնավոր բազմանիստերից ամենալավն է անդրադարձ բաժանման մեթոդի կիրառմամբ գունդ եռանկյունացնելու համար[6]։ Քանի որ այն պարունակում է դրանց մեջ ամենամեծ թվով նիստեր, ստացված եռանկյունների խեղաթյուրումը ճիշտ եռանկյունիների նկատմամբ նվազագույն է։
- Քսանանիստը օգտագործվում է որպես զառախաղ սեղանի դաշտի վրա և նշվում է d20 (զառախաղ)։
Քսանանիստանման մարմիններ
խմբագրել- Բազմաթիվ վիրուսների կոպիսիդներ (օրինակ՝ բակտերիոֆագներ և միմիվիրուս)։
Գրականություն
խմբագրել- Клейн Ф. Лекции об икосаэдре и решение уравнений пятой степени / Ф. Клейн; пер. с нем. А. Л. Городенцев, А. А. Кириллов, ред. А. Н. Тюрин. — М.: Наука, 1989. — 332 с. — ISBN 5020141976
Ծանոթագրություններ
խմբագրել- ↑ 1,0 1,1 1,2 1,3 Доказательство приведено в: Cobb, John W. (2005-2007). «The Icosahedron» (անգլերեն). Վերցված է 2014 թ․ սեպտեմբերի 3-ին.
- ↑ Селиванов Д. Ф., (1890–1907). «Тело геометрическое». Բրոքհաուզի և Եֆրոնի հանրագիտական բառարան: 86 հատոր (82 հատոր և 4 լրացուցիչ հատորներ). Սանկտ Պետերբուրգ.
{{cite book}}: CS1 սպաս․ location missing publisher (link) CS1 սպաս․ բազմաթիվ անուններ: authors list (link) CS1 սպաս․ հավելյալ կետադրություն (link) - ↑ «Euclid's Elements, Book XIII, Proposition 16».
- ↑ 4,0 4,1 Начала Евклида. Книги XI—XV. — М.—Л.: Государственное издательство технико-теоретической литературы, 1950. — Помимо перевода на русский язык сочинения Евклида это издание в комментариях содержит перевод предложений Паппа о правильных многогранниках.
- ↑ Оригинальный текст на древнегреческом языке с параллельным переводом на латинский язык: Pappi Alexandrini Collectionis. — 1876. — Vol. I. — P. 150—157.
- ↑ OpenGL Red Book Ch.2 Արխիվացված 2015-01-08 Wayback Machine



