Քվանտային վիճակ

Քվանտային վիճակ, ցանկացած հնարավոր վիճակ, որում կարող է գտնվել քվանտային համակարգը։ Մաքուր քվանտային վիճակը կարող է նկարագրվել՝

• ալիքային մեխանիկայում՝ ալիքային ֆունկցիայով,
• մատրիցային մեխանիկայում՝ տվյալ համակարգի վիճակի վեկտորով կամ քվանտային թվերի լրիվ համախմբով։

Այս նկարագրությունները մաթեմատիկորեն համարժեք են։ Ընդհանուր դեպքում քվանտային վիճակը (խառը վիճակը) սկզբունքորեն չի կարող նկարագրվել ալիքային ֆունկցիայով և պետք է նկարագրվի խտության մատրիցով, որը ոչ բացասական, միավոր հետքով ինքնահամալուծ օպերատոր է։ Քվանտային վիճակը կարող է մեկնաբանվել որպես որոշ ֆիքսված քվանտային թվերով վիճակագրական համույթ։

Էլեկտրոնի հավանականության խտությունները ջրածնի ատոմի տարբեր քվանտային վիճակներում

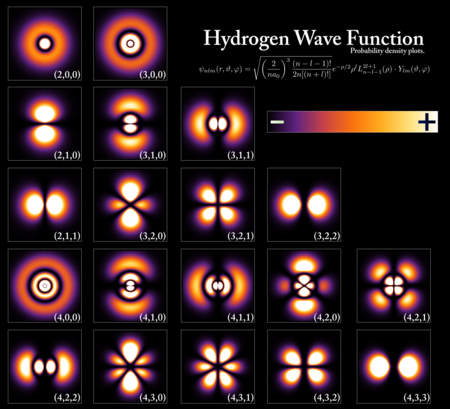
Վիճակների վեկտորներ

Տրված քվանտային համակարգի հնարավոր վիճակների համար կիրառվում է ${\mathcal {H}}$ հիլբերտյան տարածության մաթեմատիկական ապարատը, որը թույլ է տալիս գործնականում ամբողջությամբ նկարագրել համակարգի հետ տեղի ունեցող ամեն ինչ։ Քվանտային համակարգի նկարագրման համար այս դեպքում վերմուծվում է այսպես կոչված վիճակի վեկտոր, որն իրենից ներկայացնում է քվանտային համակարգն ամբողջությամբ նկարագրող մաթեմատիկական մեծությունների բազմություն։ Օրինակ, {$n\$, $\ell \$, $m_{\ell }\$, $m_{s}\,\!$} չորս թվերի բազմությունը որոշում է էլեկտրոնի վիճակը ջրածնի ատոմում, և կոչվում է էլեկտրոնի քվանտային թվեր։

Նման կառուցվածքը հնարավոր է քվանտային համակարգերի վերադրման սկզբունքի շնորհիվ։ Վերադրման սկզբունքի էությունն այն է, որ եթե գոյություն ունեն քվանտային համակարգի երկու հնարավոր վիճակներ, ընդ որում առաջին վիճակում որոշ դիտվող մեծություն կարող է ընդունել p₁, p₂, …, արժեքներ, իսկ երկրորդում՝ q₁, q₂, …, ապա գոյություն ունի նաև նրանց վերադրումը հանդիսացող վիճակ, որում այդ մեծությունը կարող է ընդունել p₁, p₂, …, q₁, q₂, …. արժեքներից ցանկացածը։ Այս երևույթի քանակական նկարագրությունը տես «Մաթեմատիկական ֆորմալիզմը» բաժնում։

Փակագծային նշանակումներ

$\psi$ վիճակին համապատասխանող վիճակի վեկտորը կնշանակենք $\left|\psi \right\rangle$։ $\psi$ վիճակին համապատասխանող համալուծ վեկտորը կնշանակենք$\left\langle \psi \right|$։ $\left|\psi \right\rangle$ և $\left|\phi \right\rangle$ վեկտորների սկալյար արտադրյալը կնշանակենք $\left\langle \phi |\psi \right\rangle$, իսկ ${\mathcal {F}}$ օպերատորի ներգործությանը ենթակա $\left|\psi \right\rangle$ վեկտորը կնշանակենք ${\mathcal {F}}\left|\psi \right\rangle$։ $\left\langle \psi \right|$ սիմվոլը կոչվում է բրա (անգլ bra), իսկ իսկ $\left|\psi \right\rangle$-ը՝ քեթ (անգլ. ket)։ Այսպիսի նշանակումները ընդհանուր առմամբ համաձայնեցվում են գծային հանրահաշվի սովորական նշանակումներին, բայց ավելի հարմար են քվանտային մեխանիկայում, քանի որ թույլ են տալիս ավելի ակնհայտ և կարճ անվանում տալ գործածվող վեկտորներին։ Այս նշանակումներն առաջին անգամ ներմուծել է Դիրակը։ Վեկտորների անունները կազմվում են անգլ. bracket (փակագիծ) բառի մասնատման երկու հնչեղ մասերից՝ bra և ket։

Մաթեմատիկական ֆորմալիզմ

${\mathcal {H}}$ տարածության յուրաքանչյուր ոչ զրոյական վեկտոր համապատասխանում է թվային վիճակի։ Սակայն վեկտորները, որոնք տարբերվում են միայն ոչ զրոյական կոմպլեքս թվի բազմապատկիչով, համապատասխանում են մեկ ֆիզիկական վիճակի։ Երբեմն ենթադրում են, որ $|\psi \rangle$ վիճակի վեկտորը պետք է անպայման նորմավորված լինի մեկի. $\langle \psi |\psi \rangle =1$՝ ցանկացած ոչ զրոյական վեկտոր ձեռք է բերում այս հատկությունը, եթե բաժանենք այն իր նորմի վրա. ${\sqrt {\langle \psi |\psi \rangle }}$։

Երկու տարբեր վիճակներ դիտարկելիս նրանց համապատասխան վեկտորների զույգերի վերադրումը (բոլոր հնարավոր գծային կոմբինացիաները) երկչափ գծային կոմպլեքս տարածություն է տալիս։ Ֆիզիկական վիճակների համապատասխան բազմությունը կլինի երկչափ մակերևույթ՝ Ռիմանի ոլորտ։

Երկու ենթահամակարգերից բաղկացած քվանտային համակարգի դիտարկման ժամանակ վիճակների տարածությունը կազմավորվում է թենզորական արտադրյալի տեսքով։ Նման համակարգերը, բացի իրենց ենթահամակարգերի վիճակների կոմբինացիայից, ունեն նաև խճճված վիճակներ։

Վիճակների թիվը

Եթե համակարգն ունի գոնե երկու ֆիզիկապես տարբեր վիճակներ, ապա հնարավոր վիճակի վեկտորների բազմության հզորությունը (նույնիսկ կոմպլեքս թվով բազմապատկիչի ճշտությամբ) հասկանալիորեն անվերջ է։ Սակայն Քվանտային համակարգի վիճակների թիվ ասելով հասկանում են գծայնորեն անկախ վիճակների թիվը, այսինքն՝ ${\mathcal {H}}$ տարածության չափականությունը։ Դա համապատասխանում է ինտուիցիային, քանի որ նկարագրում է չափումների հնարավոր ելքերի թիվը, բացի այդ, թենզորական արտադրյալի ժամանակ (այսինքն, բաղադրյալ համակարգի կառուցման ժամանակ) տարածությունների չափականությունները բազմապատկվում են։

Փակ քվանտային համակարգ դիտարկելու կոնտեքստում (այսինքն՝ Շրյոդինգերի հավասարումը) վիճակներո ասելով կարող ենք հասկանալ միայն ստացիոնար վիճակները՝ համիլտոնյանի սեփական վեկտորները, որոնք համապատասխանում են տարբեր էներգիական մակարդակներ։ Վերջավոր չափողականությամբ ${\mathcal {H}}$ տարածության դեպքում և այլասերման բացակայության ժամանակ էներգիական մակարդակների (և նրանց համապատասխան վիճակների) թիվը հավասար կլինի տարածության չափողականությանը։

Մաքուր վիճակ

Մաքուր վիճակը ամբողջությամբ ցույց տրված քվանտային վիճակն է։ Եթե տվյալ քվանտային օբյեկտը (օրինակ, ինչ-որ տարրական մասնիկ) մաքուր վիճակում է, դա նշանակում է, որ մենք ունենք նրա մասին ամբողջ ինֆորմացիան։ Միայն մաքուր վիճակները կարող են լիովին նկարագրվել ալիքային ֆունկցիայով։

Գրականություն

• Березин Ф. А., Шубин М. А. Уравнение Шредингера. М.։ Изд-во МГУ, 1983. 392с.
• Боум А. Квантовая механика։ основы и приложения. М.։ Мир, 1990. — 720 c. Глава IV.
• Дирак П. Принципы квантовой механики. 2-е изд. М.: Наука, 1979. — 480 с.
• Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.։ Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5.