Եռաչափ տարածություն
Եռաչափ տարածություն` նյութական աշխարհի երկրաչափական մոդելն է։ Այս տարածքությունը կոչվում է եռաչափ, քանի որ այն ունի երեք միասնական չափեր՝ երկարություն, լայնություն և բարձրություն, այսինքն ՝ եռաչափ տարածությունը նկարագրվում է երեք միավոր ուղղանկյուն վեկտորներով։ Եռաչափ տարածության մասին մարդու պատկերացումը ձևավորվում են դեռ վաղ մանկությունից և այն կապված է մարդու շարժումների կոորդինացիայի հետ։ Զգայարանների միջոով մեզ շրջապատող աշխարհը ընկալելու կարողությունը անվանում են խորության ընկալում։

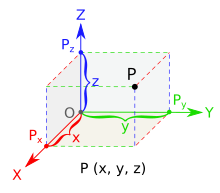
Վերլուծական երկրաչափության մեջ եռաչափ տարածության յուրաքանչյուր կետը նկարագրվում է երեք մեծությունների՝ կոորդինատների միջոցով։ Տրվում են երեք փոխուղղահայաց կոորդինատային առանցքներ, որոնք հատվում են հաշվարկման սկզբնակետում։ Կետի դիրքը նշվում է այս երեք առանցքների նկատմամբ ունեցած դիրքով՝ թվերի կարգավորված եռյակի միջով։ Այս թվերից յուրաքանչյուրը ցույգ է տալիս համապատասխան առանցքի երկայնքով հաշվարկման սկզբնակետից կետի ունեցած հեռավորությունը։
Կան նաև այլ կոորդինատային համակարգեր, որոնցից առավել հաճախ օգտագործվում են գլանաձև և գնդաձեւ համակարգեր։
Մեկ այլ տեսակետ է տալիս գծային հանրահաշիվը, որտեղ կարևոր դեր է խաղում գծային անկախության հասկացությունը։ Տիեզերքը եռաչափ է, քանի որ տուփի բարձրությունը կախված չէ նրա երկարությունից և լայնությունից։ Գծային հանրահաշվի լեզվով ասած․ տարածությունը եռաչափ է, քանի որ յուրաքանչյուր կետ կարող է տրվել երեք գծայնորեն անկախ վեկտորների միջոցով։ Այս առումով տարածություն-ժամանակ համակարգը քառաչափ է, քանի որ ժամանակ մեջ կետի դիրքը կախված չէ տարածության մեջ նրա ունեցած դիրքից։
Եռաչափ տարածությունն ունի մի քանի հատկություններ, որոնց շնորհիվ այն տարբերում է այլ չափերի տարածություններից։ Օրինակ, նա ամենափոքր չափի տարածությունն է, որի մեջ դուք կարող եք հանգույց կապել պարանի մի կտորից[1]։ Ֆիզիկայի շատ օրենքներ, օրինակ, հակադարձ քառակուսիների շատ օրենքներ կապված են այն բանի հետ, որ մեր տարածությունը եռաչափ է[2]։
Զրոական, միաչափ և երկչափ տարածությունները կարելի է համարել եռաչափ տարածության մասնավոր դեպքեր։ Իսկ եռաչափ տարածությունը կարելի է համարել քառաչափ տարածության մոդելի մի մաս(չորրորդ չափումը երբեմն անվանում են ժամանակ)[3]։
Ծանոթագրություններ
խմբագրել- ↑ Dale Rolfsen, Knots and Links, Publish or Perish, Berkeley, 1976, ISBN 0-914098-16-0
- ↑ Brian Greene, The Fabric of the Cosmos, Random House, New York, 2003, ISBN 0-375-72720-5
- ↑ «Четырёхмерное пространство — время». Վերցված է 2009 թ․ փետրվարի 26-ին.