Շտայնհաուզ-Ջոնսոն-Թրոթթեր ալգորիթմ

Շտայնհաուզ Ջոնսոն Թրոթթեր (Steinhaus–Johnson–Trotter) ալգորիթմը, որը նաև կոչվում է պարզ փոփոխություններ, անվանվել է Ուգո Շտայնհաուզի (Hugo Steinhaus), Սելմեր Մ. Ջոնսոնի (Selmer M. Johnson) և Հեյլ Ֆ. Թրոթթերի (Hale F. Trotter) անվամբ։ Այս ալգորիթմ կատարում է բոլոր n էլեմենտների վերադասավորում։ Յուրաքանչյուր վերադասավորում կատարվում է այն հաջորդականությամբ, որ դրա առաջացումը տարբերվում է նախորդ վերադասավորումից 2 հարևան տարրերի հաջորդականությունը փոխանակելով։ Համարեքորեն, այս ալգորիթմը գտնում է Համիլտոնյան ճանապարհ բազմանիստում։

Շտայնհաուզ-Ջոնսոն-Թրոթթեր ալգորիթմ
Տեսակ	կոմբինատորային ալգորիթմ և mathematical concept?
Անվանված է	Hale F. Trotter?, Հուգո Շտայնհաուս և Selmer M. Johnson?

The Hamiltonian path in the Cayley graph of the symmetric group generated by the Steinhaus–Johnson–Trotter algorithm

Այս մեթոդը հայտնի էր դեռևս 17-րդ դարի զանգերի փոփոխությամբ և Sedgewick (1977)–ը կոչում է այն «հավանաբար ամենահայտնի այգորիթմը թվարկումների վերադասավորմամբ»։ Ինչպես նաև այն պարզ է և արդյունավետ, ունի մի առավելությունը, ըստ որի կարող է հետագա հաշվարկների վերադասավորման վերաբերյալ արագությունը մեծացնել, վերադասավորումների՝ միմյանց այդքան նման լինելու պատճառով։

Ռեկուրսիվ կառուցվածք

Վերադասավորումների հերթականությունը տրված n շարքի համար կարող է ձևավորել n-1 շարքի հերթականությունից n թիվը դնելով յուրաքանչյուր հնարավոր դիրքում։ Երբ n-1 միավորների վերադասավորումը հավասարաչափ է, ապա n թիվը տեղադրվում է բոլոր հնարավոր դիրքերում նվազման կարգով, n-ով իջնելով 1, երբ n-1 միավորների թիվը կենտ է, n թիվը տեղադրվում է բոլոր հնարավոր դիրքերում աճման կարգով։

Այսպիսով մեկ վերադասավորումից մեկ տարր.

1

Կարելի է 2 թիվը տեղադրել յուրաքանչյուր հնարավոր դիրքում նվազման կարգով՝ ձևավորելով 2 տարրերի վերադասավորումով ցուցակ.

1 2

2 1

Հետո կարելի է 3 թիվ տեղադրել յուրաքանչյուր 3 տարբեր դիրքերում, իրենց 3 դասավորություններով, նվազման կարգով առաջին վերադասավորման համար 2 1, և հետո աճման կարգով 1 2 ։

1 2 3

1 3 2

3 1 2

3 2 1

2 3 1

2 1 3

Ռեկուրսիայի հաջորդ փուլը, 4 թիվ տեղադրված կլինի նվազման կարգով 1 2 3- ից, աճման կարգով հաշվի 1 3 2 – ից, նվազման կարգով հաշվի 3 1 2 և այլն։ Նույն տեղաբաշխման օրինակով, նվազման և աճման միջև փոփոխվող տեղաբաշխումը n-ից, կիրառելի է n–ի ցանկացած ավելի մեծ արժեքի համար։ Այսպիսով, յուրաքանչյուր տեղաբաշխում իր նախորդից տարբերվում է կամ մի դիրքում ժամանակի ընթացքում n–ի մի անգամյա շարժմամբ, կամ 2 փոքր համարների փոփոխությամբ, ժառանգված նախորդ հաջորդականությամբ ավելի կարճ տեղաբաշխումից։ Ամեն դեպքում այդ տարբերությունը ընդամենը երկու հարակից տարրերի փոփոխությունն է։ Երբ n>1 առաջին և վերջին տարրերի հաջորդականությունը նույնպես երկու հարակից տարրերի տարբերութուն է (1 և 2 համարների դիրքերը), որոնք կարող են հեշտությամբ ցուցադրված լինել եզրակացությունում։

Թեև այս հաջորդականությունը կարող է գեներացվել է ռեկուրսիվ ալգորիթմի, որը կառուցում էր փոքր տեղաբաշխմամբ հաջորդականություն և ապա կատարում բոլոր հնարավոր զետեղումները խոշորագույն թվաքանակով ռեկուրսիվ գեներացված հաջորդականության մեջ։ Փաստացի Շտայնհաուզ Ջոնսոն Թրոթթեր (Steinhaus–Johnson–Trotter) ալգորիթմր խուսափում է ռեկուրսիայից, փոխարեն հաշվելով նույն տեղաբաշխման հաջորդականությունը կրկնվող մեթոդով։

Ալգորիթմ

Ինչպես նկարագրված է Ջոնսոն-(1963)-ում, որ ալգորիթմի համար առաջացնող հաջորդ հաջորդականությունը π-ն հատկապես պարզ է.

• Յուրաքանչյուր 1 - i մինչև N, թող լինի X i դիրքորոշումը, որտեղ i արժեքը տեղադրված է π հաջորդականությունում։ Եթե կարգը համարների 1 - i 1-ին հաջորդականության π սահմանում է, թող Yi = XI - 1, հակառակ դեպքում, թող Yi = XI + 1։ Գտնել ամենամեծ i թիվը, որոնց համար yi սահմանում վավերական է π հաջորդականությունը, որոնք պարունակում են մի շարք ավելի փոքր, քան i-ն։ Փոխանակել արժեքների դիրքերը xi և yi։
• Երբ որևէ տեղ չենք կարող գտնել համար i ալգորիթմի երկրորդ քայլի պայմաններին հանդիպելով, ալգորիթմը հասնում է վերջնական հաջորդականությանն ու դադարում։ Սույն կարգը կարող է իրականացվել O(n) յուրաքանչյուր անգամ հաջորդականությունում։

Թրոթթերը (Trotter) (1962) տալիս է այլընտրանքային իրականացնում կրկնվող ալգորիթմին նույն հաջորդականությամբ։

Արագացումը

Շիմոնի կողմից հետագա բարելավումը, նույնիսկ նախատեսում է բարելավել վարման ժամանակը ալգորիթմի միջոցով պահելու լրացուցիչ տեղեկություններ՝ յուրաքանչյուր տարրի քանակը հաջորդականության մեջ, և ուղղություն (դրական, բացասական կամ զրո), որում այժմ շարժվում է (ըստ էության, սա այն նույն ինֆորմացիան հաշվարկում է օգտագործելով հավասարություն է Ջոնսոնի ալգորիթմի տարբերակով)։ Ի սկզբանե այդ ուղղությունը թվի 1 - ի զրոյական է, և մյուս բոլոր տարրերը ունեն բացասական ուղղություն։ 1 -2 -3 Յուրաքանչյուր քայլում ալգորիթմը գտնում է ամենամեծ տարրը հետ ոչ զրոյի ուղղությամբ, և տեղափոխում այն նշված ուղղությամբ։ 1 -2 -3 Հետո ամեն քայլափոխի բոլոր տարրերը ավելի մեծ են քան ընտրված տարրը, ունեն սահմանված ուղղություններ՝ դրական կամ բացասական։ Այսպես, այս օրինակում, երբ 2 համարը շարժվում է, 3 համարը դառնում է նշված ուղղությամբ ևս։ 2 +3 1 Ալգորիթմի մնացած երկու քայլերը n = 3 համար են. 2 +3 1 1 2 3

Երբ բոլոր համարները դառնում են չնշված, ապա ալգորիթմը դադարում է։

Այս ալգորիթմը տանում է անգամ հաղորդագրությունները O (i) յուրաքանչյուր քայլի համար, որի ընթացքում ամենամեծ թվով շարժվել է n - i + 1-ը։ Այսպիսով, փոխանակումներն ընդգրկող համարը փակցնելու համար պետք է ոչ միայն մշտական ժամանակ, միջին ժամանակը մեկ հաջորդականությամբ գեներացված նույնպես հաստատուն է, թեև փոքր համարը կարող է վերցնել ավելի մեծ քանակությամբ ժամանակ։

Նույն գործընթացի ավելի բարդ առանց հանգույցի տարբերակը թույլ է տալիս իրականացնել դա հաստատուն ժամանակում ամեն դեպքում, սակայն փոփոխությունների համար անհրաժեշտ է վերացնել հանգուցներն այն կարգով, որոնք գործնականում դանդաղ են։

The algorithm defines a Hamiltonian path in a Cayley graph of the symmetric group. The inverse permutations define a path in the permutohedron։
	Permutohedron
Permutations form a Gray code. The swapped elements are always adjacent.	Permutations, inversion vectors and inversion sets form a Gray code.
Permutations with green or orange background are odd. The smaller numbers below the permutations are the inversion vectors. Red marks indicate swapped elements. Compare list in natural order.

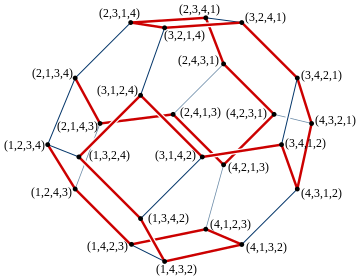
Երկրաչափական ներկայացում

n տարրերց բաղկացած բոլոր հաջորդականությունների այդ փաթեթը կարող է ներկայացված լինել երկրաչափորեն, վեկտորի հաջորդականությամբ(1, 2, ... n)։ Չնայած այս կերպով սահմանված է n ծավալային տարածության մեջ, դա իրականում (n-1) տարածական պոլիտոպ է։ Եթե ամեն գագաթ պիտակավորված է, իր գագաթի կոորդինատներով սահմանված շրջված հաջորդականության համար, որի արդյունքում պիտակավորումը նկարագրում է սիմետրիկ խմբից Քեյլիի գրաֆիկը։ Այսպես, յուրաքանչյուրը երկու հարևան հաջորդականություններ առաջացել են Շտայնհաուզ Ջոնսոն Թրոթթեր (Steinhaus–Johnson–Trotter) ալգորիթմի կողմից։ Եթե հաջորդականությունների հերթականությունը ավարտվում է ավելացնելով մեկ եզրը վերջին հաջորդականությունից դեպի առաջին, ապա դրա արդյունքը Համիլտոնյան ցիկլի փոխարեն է։

Գրեյ (Gray) կոդերի կապը

Գրեյ կոդը տրված արմատով հաջորդական թվերի համար է, որը պարունակում է բոլոր համարները, մինչև տվյալ սահմանաչափի ճիշտ մեկ անգամ, այնպես որ յուրաքանչյուր զույգ հաջորդական թվերը տարբերվեն մեկ նիշով։ 1-n թվերի հաջորդականությունը կարող է տեղադրվել մեկով 1-ի հետ, նամակագրության n! համարները 0 - ի n! - 1 - ի յուրաքանչյուր հաջորդականության ci թվերի հետ, որը հաշվարկում է դիրքերի թվի հաջորդականությունում, որն i արժեքից դեպի աջ գտնվող արժեքն է և որը պարունակում է մեկ արժեքով պակաս, քան I-ն, և հետո այս հաջորդականությունը մեկնաբանվում է ֆակտորիալ համակարգի թիվ, այսինքն, խառը համակարգ լրիվ հաջորդականությամբ (1, 2, 3, 4, ...). Օրինակ (3, 1, 4, 5, 2) հաջորդականությունը կտա c1= 0, C2 = 0, c3 = 2, c4 = 1 և C5 = 1 արժեքները։ Այդ արժեքների հերթականությունը՝ (0, 0, 2, 1, 1), համարը տալիս՝ 0 × 0! + 0 × 1! + 2 × 2. + 1 × 3. + 1 × 4. = 32։

Հետևողական հաջորդականությունները շարքում առաջացել են Շտայնհաուզ Ջոնսոն Թրոթթեր (Steinhaus–Johnson–Trotter) ալգորիթմի կողմից, ունեն համարներ, որոնցով տարբերվում են, ձևավորելով մի Գրեյ կոդը ֆակտորիալ թվերի համակարգի համար։

Ընդհանուր առմամբ, համակցական ալգորիթմեր հետազոտողները սահմանել են Գրեյ կոդը մի շարք համակցական օբյեկտներ պատվիրելու համար, օբյեկտների, որոնց յուրաքանչյուր երկու հաջորդական առարկաները տարբերվում են նվազագույն կերպով։ Ընդհանուր առմամբ, Շտայնհաուզ Ջոնսոն Թրոթթեր (Steinhaus–Johnson–Trotter) ալգորիթմն ստեղծել է Գրեյ կոդը իրենց հաջորդականությունների համար։

Պատմություն

Այս ալգորիթմն անվանվել է Հյուգո Շտայնհաուզի (Hugo Steinhaus), Սելմեր Մ. Ջոնսոնի (Selmer M. Johnson) և Հեյլ Ֆ. Թրոթթերի (Hale F. Trotter) անվամբ։ Ջոնսոնը և Թրոթթերը հայտնաբերել են 1960–ականների սկզբին միմյանցից անկախ։ Շտայնհաուզի գրքերից մեկը, որն սկզբնապես տպագրվել է 1958 թվականին և թարգմանվել է անգլերեն 1963 թվականին, նկարագրում է համապատասխան շփոթություն առաջացնող բոլոր հաջորդականությունների համակարգերը մասնիկների համակարգի միջոցով, հաստատուն արագությամբ յուրաքանչյուր շարժում մի գծի հետ՝ փոխանակելով պաշտոնները, երբ մի մասնիկը հասնում է մյուսին։ Լուծումը հնարավոր չէ, երբ n > 3, քանի որ թիվը փոխանակվում է հաւորդականության ավելի փոքր թվով, բայց Շտայնհաուզ Ջոնսոն Թրոթթեր (Steinhaus–Johnson–Trotter) ալգորիթմը նկարագրում է մասնիկների միջնորդությունը ոչ մշտական արագության հետ, որը առաջացնում է բոլոր հաջորդականությունները։ Մաթեմատիկայից դուրս, այս նույն մեթոդը երկար ժամանակ հայտնի է եղել որպես եկեղեցական զանգերը փոխելու մեթոդ, այն տալիս է մի կարգ, ըստ որի զանգերի փաթեթը կարող է զնգալ հնարավոր բոլոր հաջորդականությունների միջոցով։ Դրանք, այսպես կոչված, "պարզ փոփոխություններ են", որոնք արձանագրվել են դեռեւս 1621 թվականին չորս զանգերի համար, և 1677 թվականին Ֆաբիան Ստեդմանի (Fabian Stedman) գրքերից մեկը թվարկում էր լուծումները մինչև վեց զանգերի համար։ Զանգերը փոխելուց մնացել է մի կանոն, որ զանգը չի կարող մնալ նույն դիրքում երեք հաջորդականությունների համար, այս կանոնը խախտվել է պարզ փոփոխությունների կողմից, որպեսզի այլ ռազմավարությունները, որոնք փոփոխում են բազմաթիվ զանգերը մեկի նախագծված լինեին։

Առնչություններ

• Dershowitz, Nachum (1975), «A simplified loop-free algorithm for generating permutations», Nordisk Tidskr. Informationsbehandling (BIT), 15 (2): 158–164, MR 0502206.
• Dijkstra, Edsger W. (1976), «On a gauntlet thrown by David Gries» (PDF), Acta Informatica, 6 (4): 357–359, doi:10.1007/BF00268136, MR 0426492. Although DIjkstra does not cite any prior literature, an earlier draft EWD502 reveals that he knew of Trotter (1962).
• Ehrlich, Gideon (1973), «Loopless algorithms for generating permutations, combinations, and other combinatorial configurations», Journal of the ACM, 20 (3): 500–513, doi:10.1145/321765.321781.
• Even, Shimon (1973), Algorithmic combinatorics, Macmillan.
• Johnson, Selmer M. (1963), «Generation of permutations by adjacent transposition», Mathematics of Computation, 17: 282–285, doi:10.1090/S0025-5718-1963-0159764-2, JSTOR 2003846, MR 0159764.
• Knuth, Donald (2004), «A Draft of Section 7.2.1.2: Generating All Permutations», The Art of Computer Programming, Pre-Fascicle 2B, Արխիվացված է օրիգինալից 2012 թ․ մարտի 30-ին, Վերցված է 2012 թ․ մայիսի 31-ին.
• McGuire, Gary (2003), Bells, motels and permutation groups.
• Savage, Carla (1997), «A survey of combinatorial Gray codes», SIAM Review. A Publication of the Society for Industrial and Applied Mathematics, 39 (4): 605–629, doi:10.1137/S0036144595295272, JSTOR 2132693, MR 1491049.
• Sedgewick, Robert (1977), «Permutation generation methods», ACM Comput. Surv., 9 (2): 137–164, doi:10.1145/356689.356692.
• Steinhaus, Hugo (1964), One hundred problems in elementary mathematics, New York: Basic Books, էջեր 49–50, MR 0157881.
• Trotter, H. F. (1962 թ․ օգոստոս), «Algorithm 115: Perm», Communications of the ACM, 5 (8): 434–435, doi:10.1145/368637.368660.

Արտաքին կապեր

• Counting And Listing All Permutations: Johnson–Trotter Method at cut-the-knot